Ю.В.Адамчук, В.В.Титов
Аннотация
Рассмотрены основные физические процессы, ответственные за электризацию газопепловой тучи над вулканом. Анализируются некоторые особенности механики вулканического аэрозоля и его гравитационной сепарации. Показано, что наиболее важными среди множества физических и физико-химических процессов возникновения и разделения зарядов в вулканическом облаке являются термоэлектронная эмиссия и термоэлектричество. Рассчитаны основные закономерности электризации аэрозольных частиц при этих процессах. Установлено, что для образования молний в вулканической туче материал выброса должен в заметном количестве содержать мелкодисперсную фракцию (1-30 мкм). Коротко проанализированы возможности участия других физических процессов в электризации аэрозольных частиц и вулканического облака в целом. Рассмотрены также кинетика разделения зарядов и условия образования молний в вулканических тучах. Показана связь интенсивности электрических процессов с энергией и мощностью извержения. Сделан вывод о необходимости комплексного характера измерений электрической активности гаэопепловых туч вместе с исследованием кинетики выноса массы и определением начальной температуры материала выброса.
ВВЕДЕНИЕ
Электрические явления в аэрозолях весьма разнообразны как по виду, так и по интенсивности. Наиболее грандиозно протекают электрические процессы в природных аэрозолях при больших объемах (исчисляемых десятками и сотнями тысяч кубометров) и высоких напряжениях (до сотен мегавольт) [1, 2]. Частота молний в грозовых тучах иногда достигает 0,05 — 0,2 с-1. Однако самая высокая интенсивность электрических процессов наблюдается в сухих газопепловых тучах над вулканами (см. библиографию в работе [3]). Ежесекундные крупные молнии (одна из которых показана на рис. 1), гораздо более частые мелкие искровые разряды длиной 8 — 10 м, интенсивное и длительное коронное свечение в районах, накрытых вулканической тучей, - вот краткий перечень тех явлений, которые наблюдались при вулканических извержениях.
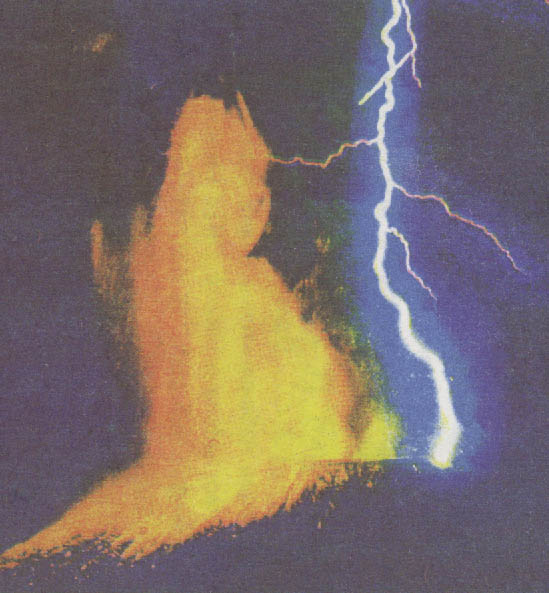
Рис.1. Молния над кратером во время Большого Трещинного Толбачинского извержения 1975 г. Северный прорыв. Фото В.Е.Гиппенрейтера.
Далеко не всякое извержение сопровождается молниями. Это значит, что интенсивность электризации вулканического аэрозоля существенным образом зависит от характеристик извержения. Вообще говоря, электризация аэрозольных частиц может происходить по многим причинам, связанным с физическими и физико-химическими процессами в газошлакопепловой туче {3, 4]. Однако ввиду того, что интенсивность электризации вулканического аэрозоля значительно выше, чем всех других известных аэрозолей [3 — 6], можно, вероятно, выделить ряд специфических процессов, которые играют основную роль именно в вулканическом облаке.
Наиболее существенными особенностями вулканического аэрозоля являются:
В данной работе рассмотрены два механизма электризации шлакопепловых вулканических частиц, а именно — термоэмиссия электронов и термоэлектричество. Расчет процесса термоэлектронной эмиссии позволяет определить минимальную начальную температуру Tmin материала выброса, ниже которой интенсивность термоэмиссии настолько мала, что уже не в состоянии обеспечить заметную электризацию. Длительность действия термоэмиссионного механизма определяется временем остывания частиц от начальной температуры до фиксированной Тmin и может варьироваться от ~0,1 до ~10 с. Показано также, что термоэлектрический механизм электризации частиц вулканического аэрозоля не имеет температурного "порога", поэтому интервал действия этого механизма по температуре больше, чем термоэмиссионного, а временной интервал обусловлен временем разбавления аэрозоля и почти постоянен (~1,5 с).
Хотя по скорости генерации заряда термоэлектрический механизм электризации иногда уступает термоэмиссионному, но по диапазону действия он значительно шире, так как функционирует в любых аэрозолях, если есть разность температур соприкасающихся частиц D T ~ ~ 10 К и выше. Показано также, что другие механизмы электризации, обсуждавшиеся в литературе (пьезоэлектричество, баллоэлектрический эффект, трение частиц и газовых струй и т.д.), не могут играть заметной роли в образовании электрического заряда и молний над вулканами, прежде всего по причине отсутствия направленности этих процессов, необходимой для накопления и разделения заряда в макроскопическом масштабе. Напомним, что для возникновения молний необходимы два процесса: электризация частиц в микроскопическом масштабе и разделение зарядов в масштабе всего облака. Второй из них более длительный, поэтому молнии возникают намного позже начала выброса.
Макроскопические процессы рассмотрены в настоящей работе более конспективно. Сложность процессов седиментации и сепарирования заряженного аэрозоля в условиях турбулентного перемешивания разномасштабных клубов вулканического облака не позволяет провести строгий расчет, поэтому мы ограничились привлечением (там, где это возможно) аналогии с процессами в грозовых облаках. В результате сформулированы критерии, выполнение которых необходимо для возникновения молний разного масштаба.
В работе приведен пример ретроспективного анализа первичных электрических характеристик извержения по измеренным "вторичным" эффектам активности вулкана и сделан вывод о необходимости комплексных измерений разнородных характеристик.
|
"...Мы, люди на Земле, слишком малы и не можем прочищать свои вулканы. Вот почему они доставляют нам столько неприятностей".
|
1. МЕХАНИКА ВУЛКАНИЧЕСКОГО АЭРОЗОЛЯ
В работе [4] приводится качественное описание и некоторые количественные характеристики процессов, сопровождавших образование молний при извержении вулкана Тятя на острове Кунашир в июле 1973 г. В частности, указывается, что в единичном выбросе из жерла извергалось шлакопепловое облако с массой МS. » 300 т, которое после потери направленной скорости образовывало клубящиеся сгустки с начальным диаметром D0 - 50 ¸ 100 м. В работе [7] было установлено, что распределение частиц вулканического пепла и шлака по массам удовлетворительно описывается законом:
| (1.1) |
где NS — количество частиц в заданном объеме; m — их масса; АS — константа. Вообще говоря, эта формула удовлетворительно описывает распределение по массам любых естественных атмосферных аэрозолей [8].
Таким образом, общее число частиц NS будет равно:
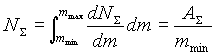 |
(1.2) |
а полная масса таких частиц MS должна равняться:
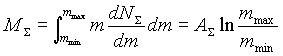 |
(1.3) |
Приближенно (с логарифмической точностью) можно положить, что mmax» 103 г, а mmin» 10-12 г (Dmin=1 мкм).
Подставляя в формулу (1.3) полную массу МS = 300 т, при логарифме ln(mmax/mmin)=34,5 находим, что константа АS = 8,7.106 г, и тогда из формулы (1.2) следует, что полное число всех частиц в шлакопепловом облаке при одном выбросе из вулкана Тятя равнялось NS = 8,7.1018 частиц со средней массой mср = 300 т/NS =3,45*10-11 г. Так как плотность пепла r п»2 г/см3, то mср[г]= r п*p Dср3/6 и средний диаметр частиц в вулканической туче Dср=3,2 мкм. Это позволяет переписать формулу (1.1) в виде:
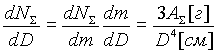 |
(1.4) |
Столь малая величина mср является следствием того, что в вулканическом облаке в основном присутствует мелкодисперсная фракция шлакопепловых частиц, хотя весовая масса твердого вещества приходится в основном на крупные частицы. (Если mmin = 10-12 г, то число частиц с m < 3,45.10-11 г = mср составляет 97%).
Результаты дальнейших расчетов сильно зависят от значения mmin, поэтому оценим величину mmin также из других соображений. На дробление частиц при выбросе тратится около 0,1% общей энергии взрыва Евзр [9]. Хотя число 0,1% сильно зависит от типа взрыва, для вулканов вариации этой величины не должны быть слишком велики из-за однотипности взрывов. Существенного различия следует ожидать лишь для катастрофических единичных взрывов и непрерывной продувки жерла, так что ошибка в определении mmin по Евзр едва ли превышает 1—2 порядка.
Поскольку суммарная поверхность всех твердых частиц выброса равна:
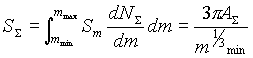 |
(1.5) |
(Sm - поверхность частицы массы m), то, полагая, что поверхностное натяжение пепловых частиц в среднем равно s s=300 дин/см [10, 11], можно вычислить увеличение поверхностной энергии частиц D Епов после дробления DЕпов=SS *ss. Приравняв D Епов затраченной энергии, равной 0,1% от Евзр, найдем:
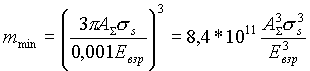 |
(1.6) |
В случае извержения вулкана Тятя в 1973 г. Евзр = 2.1017 эрг [4]. Тогда оценка минимальной массы аэрозольных частиц в вулканической туче дает величину mmin = 2*10-12 г.
Рассмотрим движение вулканических частиц в шлакопепловой туче. Следует сразу отметить, что все движение конденсированной аэрозольной частицы (любого размера) от вылета из жерла до падения на Землю можно разделить на две стадии по следующему признаку: на первой стадии частица движется ускоренно относительно окружающего объема газа, на второй стадии скорость частицы относительно окружающего газа постоянна. Длительность этих стадий определяется главным образом размером частицы и в меньшей степени — мощностью выброса. Первая, нестационарная стадия для подавляющего большинства частиц заканчивается очень рано. Обусловлена она тем, что в момент взрывного выброса (или в момент выхода газопепловой струи из жерла) газ расширяется и ускоряется, частицы же конденсированного вещества приобретают скорость лишь благодаря передаче энергии к ним от газа. Ускорение мелких аэрозольных частиц заканчивается почти сразу после окончания расширения газа, т.е. практически на высоте нескольких десятков метров. Частицы покрупнее могут разгоняться дольше, поскольку к моменту, когда давление газа в струе приблизится к атмосферному, скорость газа будет существенно выше скорости частицы. Наконец, крупные вулканические бомбы могут вообще до второй стадии не дожить: если высота подъема бомбы недостаточна для того, чтобы при падении с этой высоты она достигла равновесной скорости падения (когда устанавливается равновесие между силой аэродинамического сопротивления и силой тяжести), то от начала до конца пути бомба будет двигаться ускоренно относительно газа.
Вторая стадия — стационарное падение частицы в газе с постоянной относительно газа скоростью (сам газ вместе с рассматриваемой частицей при этом может двигаться как угодно). Ясно, что в газопепловой туче над вулканом основные процессы происходят по-разному на первой и на второй стадиях, и поэтому целесообразно оценить хотя бы ориентировочно сравнительную длительность этих стадий. Пусть к моменту, когда основное расширение газа при взрывном выбросе закончилось, различие в скоростях газа и конденсированных частиц v равно скорости звука vc (В работе [11] различие в скоростях принято равным 275 м/с). Тогда на частицу будет действовать сила, направленная вверх и равная
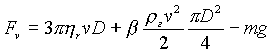 |
(1.7) |
где первое слагаемое — вязкая сила Стокса, а второе — сила динамического напора газа (с числовым множителем b = 9/2, который получается из разложения гидродинамического коэффициента сопротивления среды движущемуся телу по числам Рейнольдса [12]), третий член - сила тяжести. Нетрудно записать дифференциальное уравнение для скорости:
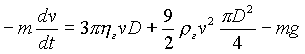 |
(1.8) |
Полное решение этого уравнения при начальном условии v (t = 0) = vc имеет вид:
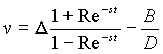 |
(1.9) |
где
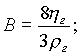 ; ; 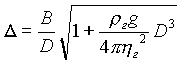 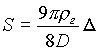 ; ; 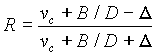 . . |
|
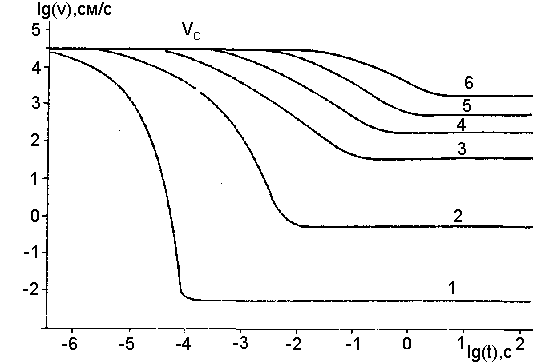 |
Рис.2. Зависимость разгона частиц разных размеров газовой струей от времени. (Начальная скорость газа относительно частиц vс=340 м/с). Размеры частиц D, см: 1 - 10-4; 2 - 10-3; 3 - 10-2; 4 - 10-1; 5 - 1; 6 - 10. |
На рис. 2 приведена зависимость v от времени исходя из (1.9) для нескольких размеров частиц. Видно, что для самых мелких частиц ускоренное движение прекращается уже через 10-4 с, в то время как самые крупные выходят на стационарный режим движения лишь через несколько секунд [5, 13].
Стационарный режим движения на рис. 2 получается, если левую часть уравнения (1.8) приравнять нулю. Решение получившегося алгебраического уравнения записывается в виде:
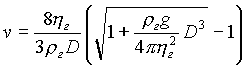 |
(1.10) |
Здесь r г и h г— соответственно плотность и вязкость газа (в котором уже кончилось адиабатическое расширение) при температуре Т = 200 С [4]. Вулканический газ состоит в основном из паров воды и составляет ~ 3% вулканического выброса по весу [11], что в нашем случае при общей массе выброса 300 т эквивалентно 9 т. Вес воздуха, занимающего объем шарового сгустка диаметром D0= 75 м, равен 290 т. Таким образом, привнесенная масса газа составляет только ~3% и, следовательно, r г = r в = 1.29.10-3 г/см3, h г = hв = 1,81.10-4 пуаз [10].
Выразив диаметр частицы D через ее массу m, окончательно получим (Формула (1.11) в таком виде встречается в [1]):
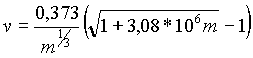 |
(1.11) |
Таким образом, вулканические бомбы массой 1 кг проходят за 1 сек 21 м, шлак массой 1 г — 6,5 м, а "средняя" аэрозольная частица облака с m = 3,45.10-11 г - 0,61 мм (рис. 3а, кривая 1). Можно отметить также, что при высоте тучи 1 км частицы массой 1 г осядут на поверхность за 2,5 мин, а частицы массой 3,45. 10-11 г — за ~ 19 суток.
Рассмотрим теперь, что изменится в этой картине, когда частицы аэрозоля станут заряженными. Перед этим заметим, что твердые частицы вулканического облака обладают огромной электрической емкостью СS , исчисляемой сотнями и тысячами фарад (емкость Земли, для сравнения, всего 7,1*10-4 Ф).
В самом деле:
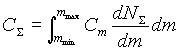 |
(1.12) |
где Cm — емкость отдельной частицы с массой m. Подставляя в (1.12) Cm = D/2 [см] и учитывая (1.1), получим, что суммарная электрическая емкость СS частиц газопепловой тучи равна
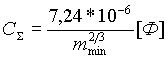 |
(1.13) |
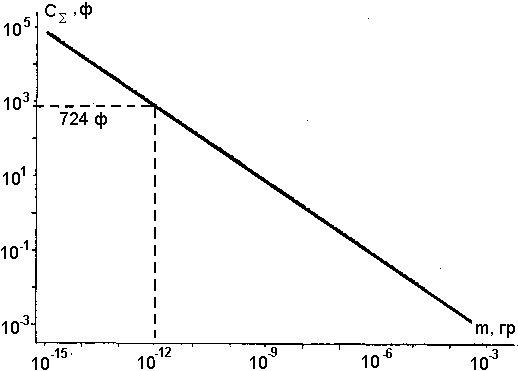
Рис.3. Зависимость суммарной электрической емкости частиц вулканического аэрозоля от степени дробления.
На рис. 3 показана зависимость СS от степени дробления аэрозоля в облаке (при mmin = 10-12 г СS = 720 Ф). Поскольку интенсивность электрических процессов и их суммарный эффект зависят от полной емкости носителей заряда, то нетрудно видеть, что электрическая активность в вулканической туче в значительной степени определяется дисперсностью аэрозоля.
Если в облаке электрического поля нет, то и процесс осаждения остается неизменным, однако, к моменту возникновения молнии поле достигает значительной величины. Пробивная напряженность поля в сухом и чистом воздухе при Т = 20° С составляет 32 кВ/см [10], но для запыленной среды с примесью воды она значительно меньше и, как и в грозовых облаках ([14], с. 287), по-видимому, не превышает. Епроб = 4 кВ/см. В электрическом поле на отрицательно заряженную частицу аэрозоля будет действовать дополнительная сила Fe » еЕ, направление которой будет совпадать с направлением силы тяжести, если в верхней части облака скапливаются отрицательные заряды, и будет противоположно силе тяжести, если вверху окажется положительный заряд. В большинстве наблюдений молнии возникали в облаках с отрицательно заряженной верхушкой, так что уравнение движения аэрозольной частицы, на которой находятся kэ лишних электронов, можно записать в виде
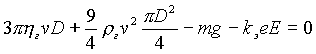 |
(1.14) |
Решение этого уравнения
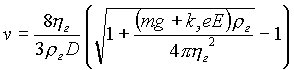 |
(1.15) |
позволяет быстро оценить величину поправки к скорости седиментации за счет электрического поля. Очевидно, эта поправка существенна только для самых мелких частиц, для которых первый член в скобке под корнем сравним со вторым. Кулоновская сила, действующая на частицу с зарядом в один электрон в электрическом поле Е = = 4 кВ/см = 13,3 эл. ст. ед., равна еЕ = 4,8.10-10 *13,3 =6,4.10-9 дин. Это значит, что "эффективная масса" частицы с одним лишним электроном увеличивается на Dm » 6,5.10-12 г. Естественно, для частицы, несущей два и более электронов, "утяжеление" будет пропорционально больше. На рис. 4 показана зависимость скорости оседания аэрозольных частиц от их размера, заряда и величины поля.
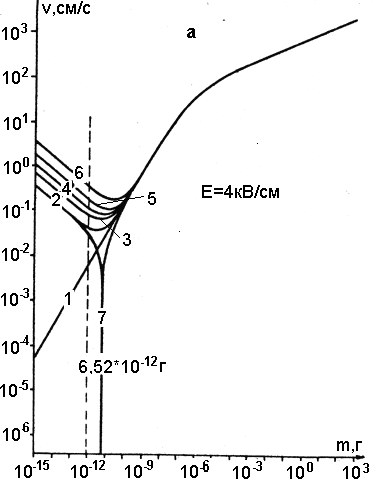 | 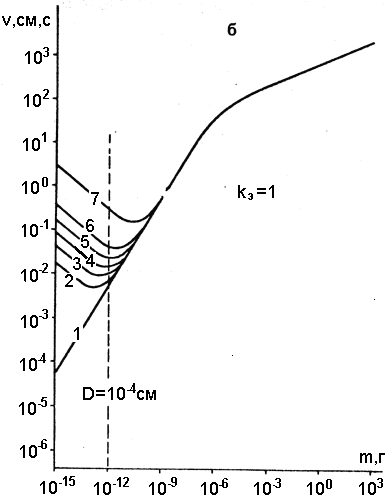 |
Рис. 4. Зависимость скорости седиментации аэрозольных частиц от массы в электрическом поле Е, направленном снизу вверх: а) - электрической поле Е=4 кВ/см, зарядовое состояние частиц: 1- незаряженные частицы, kэ=0; 2 - на частице находится один электрон, kэ=1; 3 - kэ=2; 4 - kэ=3; 5 - kэ=5; 6 - kэ=10; 7 - kэ=-1, т.е. на частице не хватает одного электрона. Нижняя часть кривой 7 (при m< 6,52*10-12 г) соответствует скорости, направленной вверх; б) - зарядовое состояние частиц kэ=1. Электрическое поле, кВ/см: 1 - Е=0; 2 - Е=0,2; 3 - Е=0,5; 4 - Е=1; 5 - Е=2; 6 - Е=4; 7 - Е=32.
Так как электрическое поле увеличивается только за счет разделения зарядов, то по мере приближения к Епроб мелкие частицы начинают все более и более тормозить процесс разделения, поскольку электрическое поле все сильнее втягивает отрицательно заряженные мелкие частички в область положительного объемного заряда облака. Однако эффект становится значительным, только когда дисперсность аэрозоля простирается в область размеров существенно меньше микрона.
Один из основных параметров любого аэрозоля — его счетная концентрация. В вулканической туче интенсивно идет разбавление аэрозоля при перемешивании объема выброса с атмосферным воздухом и рассеявшимся аэрозолем предыдущих выбросов. Вследствие этого объем, в котором рассеяно NS аэрозольных частиц выброса, постоянно увеличивается, соответственно, концентрация аэрозольных частиц падает. Вулканическая туча условно может быть разделена на четыре части:
1) струя (область после адиабатического расширения и до появления клубов);
2) область ламинарного течения газопепловых струй и быстрого движения устойчивых клубов аэрозольных частиц (зона I);
3) область турбулентных завихрений и образования облачной структуры (зона II);
4) область разрушения облачной структуры и ветрового сноса газопепловых облаков (зона III).
Поскольку это разделение условно (разные авторы проводят его по-разному [4, 15]), то для определения средней концентрации аэрозольных частиц в каждый момент времени после выброса следует учитывать, что разбавление газа выброса атмосферным воздухом происходит непрерывно.
Процесс разбавления, вероятно, можно разделить на три стадии: струя, область быстро перемешивающихся газопепловых клубов и область ветрового сноса.
Скорость разбавления аэрозоля в струе над жерлом вулкана можно оценить из следующих соображений. Видимый угол расходимости струи составляет а ~ 4°. Тогда при средней скорости струи vc ~ 300 м/с [11] и начальном диаметре струи Dс0 » 30 м объем аэрозоля будет изменяться пропорционально сечению струи, т.е.
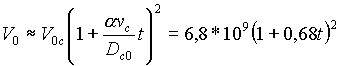 |
(1.16) |
(объем V0с = 6,8.109 см3 вычислен из массы вулканического газа 9т [4]). Этот процесс продолжается до высоты ~1000 м, т.е. в течение первых tI ~ 3 с. После этого закон разбавления изменяется.
Область, занятая быстро движущимися клубами газа, расширяется во все стороны с почти постоянной скоростью vk » 30 м/с. Это значит, что объем области увеличивается по закону
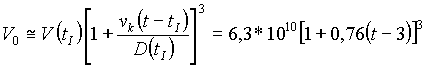 |
(1.17) |
Этот процесс длится вплоть до размера области порядка 1—2 км (tII ~ 27 с), а затем постепенно замедляется, переходя к последней, третьей стадии разбавления. Здесь следует заметить, что во время активной жизни вулкана изолированные единичные выбросы (сравнительно редкий случай), как правило, следуют друг за другом, и аэрозоль каждого последующего выброса на второй стадии разбавляется не чистым атмосферным воздухом, а в основном аэрозолем предыдущих выбросов. Это значит, что реальное изменение концентрации аэрозоля на этой стадии может быть меньше, чем дает формула (1.17).
Стадия ветрового сноса характеризуется, как и струя, постепенным увеличением видимого поперечного сечения сносимой тучи. Это увеличение происходит в основном только в горизонтальном направлении с постоянной скоростью vсн » 5 - 10 м/с, так что изменение объема подчиняется соотношению
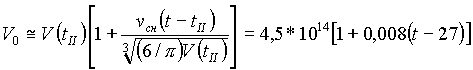 |
(1.18) |
Заметим, что на этой стадии кинетика изменения объема не зависит от того, разовый ли это выброс, серия выбросов или непрерывная струя: во всех случаях при ветровом сносе происходит разбавление чистым воздухом.
Перечисленные зависимости отображены на рис. 5. Там же показана кинетика .изменения средней счетной концентрации частиц nср шт/см3.
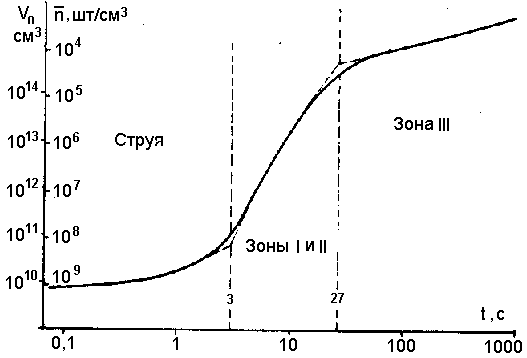
Рис.5. Зависимость изменения объема вулканического облака и счетной концентрации частиц в нем от времени.
Немаловажную роль в электрических процессах вулканической тучи играют столкновения аэрозольных частиц между собой. Процессы столкновения можно в первом приближении описать следующим образом. Отвлекаясь от зарядового влияния, будем считать, что скорость движения частицы относительно газа однозначно определяется ее размером. Тогда относительная скорость частиц размером D1 и D2 (D2>D1) равна V2— V1. Что касается эффективного сечения взаимодействия, то можно воспользоваться следующим рассуждением. Поскольку обтекание частиц газовым потоком ламинарно (Нарушение ламинарности обтекания имеет место только для крупных вулканических бомб, вклад которых в процесс электризации аэрозоля незначителен), то ламинарность сохраняется и при обтекании крупной частицы D2 потоком, содержащим мелкие частицы D1. Другими словами, частицу D1 можно считать "привязанной" к газовой струе, обтекающей D2. Будем считать также, что столкновение имеет место, если в момент максимального сближения расстояние между ними не превышает суммы их радиусов (D1 + D2)/2. Эффективное сечение струи (находясь в которой, меньшая частица столкнется с большей), конечно, меньше видимого сечения p/4(D1+ D2)2, поскольку струя при обтекании крупной частицы искривляется. Полагая сечение струи неизменным при обтекании, нетрудно прийти к выводу, что эффективное сечение столкновения равно площади кольца толщиной D1/2, окружающего частицу D2, т.е. sэф=pD1D2/2. Малую добавку pD12/4 (D1 < D2) можно для простоты отбросить, поскольку она существенна только при D1»D2, но в этом случае относительная скорость частиц близка к нулю, а значит, близка к нулю и вероятность столкновения.
Зная относительную скорость и сечение взаимодействия, можно записать выражение для вероятности столкновения данной частицы размером D2 с частицами, размер которых лежит в пределах от D1 до D1 + dD1 (D1 < D2):
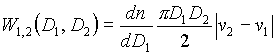 |
(1.19) |
где dn/dD1 = 1/V0 -dNS /dD1 — счетная концентрация частиц диаметром D1. Эта функция для нескольких D2 и объема облака V0 = 1012 см3 (t »5с) показана на рис. 6, из которого видно, что при расширении облака вероятность столкновения уменьшается обратно пропорционально объему облака.
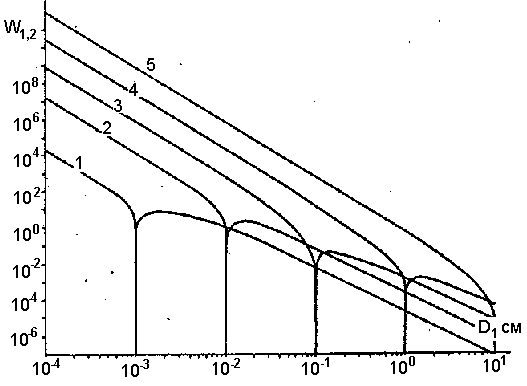 |
Рис.6. Вероятность столкновения аэрозольных частиц разного размера через 5 с после взрыва (V0=1012 см3). Размеры частиц D2, см: 1 - 10-3; 2 - 10-2; 3 - 10-1; 4 - 1; 5 - 10. |
Очевидно, число соударений частицы D2 за время dt с частицами, размер которых лежит в пределах от D1 до D1+dD1, можно вычислить, умножив W12 на dt и dD1. Интегрируя полученное дифференциальное выражение по D1, можно определять частоту соударений данной частицы с частицами из любого заданного интервала размеров D1. Нетрудно видеть, что для подавляющего большинства частиц встречи с более мелкими частицами (D1 < D2) происходят намного чаще, чем с частицами крупнее рассматриваемой (D1 > D2). На рис. 7 приведена кривая, характеризующая отношение частоты встреч с более мелкими частицами к частоте встреч с более крупными, т.е. функцию
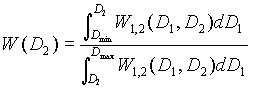 |
(1.20) |
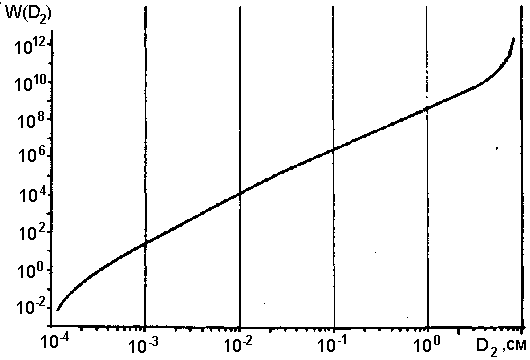 |
Рис.7. Отношение вероятности столкновения с частицей меньшего размера к вероятности столкновения с частицей большего размера для вулканического аэрозоля, дисперсный состав которого определяется формулой (1). |
Таким образом, можно считать, что любая частица размером больше 6.10-4 см сталкивается только с частицами меньших размеров [16, 17].
Приведем основные параметры вулканического аэрозоля (единичного выброса), принятые нами в расчетах. (Исходные данные для выброса взяты из [3] для извержения вулкана Тятя в 1973 г.):
|
Масса выброса МS
|
300 т |
|
Масса парогазовой смеси в одном выбросе (3% полной массы) [11] |
9 т |
|
Общее число частиц в выбросе NS |
8,7*1018 |
|
Начальная температура шлакопепловой массы |
1500К |
|
Температура газа после смешения с атмосферным воздухом |
300 К |
|
Минимальные размер Dmin и масса mmin частиц шлакопеплового облака |
1 мкм, 10-12г |
|
Максимальные размер Dmax и масса mmax частиц шлакопеплового облака |
10 см, 1 кг |
|
Суммарная поверхность аэрозольных частиц SS
|
8,19*1011 см2 |
|
Общая электрическая емкость аэрозольных частиц СS
|
720 Ф |
|
Пробивная напряженность Епроб электрического поля в газопепловой смеси вулканического облака [14] |
4 кВ/см = 13 эл. ст. ед. |
|
Плотность шлакопепловых частиц r п |
2 г/см3. |
Объем выброса и счетная концентрация аэрозоля на различных стадиях развития тучи (струя, зоны I, II и III) приведены на рис. 5.
2. ЭЛЕКТРИЗАЦИЯ ЧАСТИЦ ВУЛКАНИЧЕСКОГО АЭРОЗОЛЯ
"Вкруг скал огнистой лентой вьется
М.Ю. Лермонтов "Гроза" |
Для того, чтобы в вулканическом облаке произошел электрический разряд (молния), необходимо, чтобы возникли в достаточном количестве разноименные электрические заряды, которые должны быть разделены в пространстве в макроскопическом масштабе (порядка размеров клуба облака). Электризация аэрозольных частиц и разделение разноименных зарядов на макроскопические расстояния определяются различными процессами в газопепловой туче. Что касается макроскопического разделения зарядов, то за это ответственно гравитационное сепарирование частиц разной массы (см. формулы (1.10) и (1.15), соответственно, для нейтрального и заряженного аэрозоля), и этот вопрос мы рассмотрим ниже. В настоящем разделе остановимся на микроскопических процессах электризации отдельных частиц. Поскольку электризация в той или иной мере связана с температурой частиц, то для начала рассчитаем кинетику остывания частиц вулканического аэрозоля. В момент выброса из жерла вулкана температура газа, а также твердых и жидких фракций одинакова, однако адиабатическое расширение (от нескольких десятков до 1 атм) резко охлаждает газ, так что вулканическое облако через некоторое время после выброса представляет собой смесь охлажденного газа и относительно нагретых твердых частиц. Температура и скорость остывания частиц пепла зависят от их размеров, при этом температура более крупной частицы выше, чем частиц меньшего размера.
Зависимость изменения температуры частиц от времени может быть оценена из решения краевой задачи теплопроводности для сферических областей. Пусть сферическая частица диаметром D в начальный момент имеет по всему объему температуру Т1, а температура окружающей среды постоянна и равна Т2 (D Т = T1 — Т2). С поверхности нагретой частицы происходит непрерывный конвективный теплообмен с окружающим газом с коэффициентом теплообмена a .
Уравнение теплопроводности в силу радиальной симметрии записывается в виде:
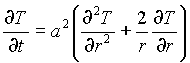 |
(2.1) |
(а2 — коэффициент температуропроводности аэрозольных частиц при граничном условии:
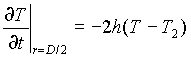 , 0£
t < , 0£
t < |
(2.2) |
где h = a /2la, la - коэффициент теплопроводности частиц. Решение получается в виде ряда по собственным функциям оператора Лапласа для сферы
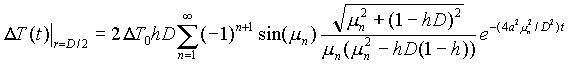 |
(2.3) |
Здесь m п — положительные корни уравнения
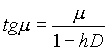 |
(2.4) |
а константы, входящие в (2.1), выбраны из следующих соображений: коэффициент теплопроводности la = 3*10-4 кал/(см.с.град) как среднее между величинами для пемзы (6.10-4 кал/(см.с.град) [18]) и шлаковаты (10-4 кал/(см.с.град) [10]); удельная теплоемкость Сp= 0,26 кал/(г.град) - величина, характерная для лавы [10]; коэффициент теплообмена a от частицы воздуху, по данным [19], меняется для разных веществ от 4.10-4 до 16.10-4 кал/(см2.с.град) — мы будем пользоваться средним значением a = 1,0.10-3 кал/(см2.с.град) - коэффициент h в уравнениях (2.2) и (2.3) равен h=a/2la =1,67 см-1; коэффициент температуропроводности а2 = l/срr п=6.10-4 см2/с.(В работе [4] принято, что а2=5*10-5 см2/с)
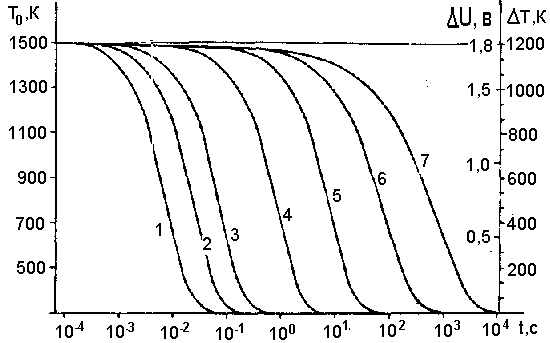 |
Рис.8. Зависимость остывания аэрозольных частиц разных размеров от времени. По оси ординат слева отложена температура частиц Т0, К, справа - разность температуры частиц и окружающего газа DТ и термоэ.д.с. DU горячих частиц относительно частиц, находящихся при комнатной температуре. Масыы частиц, г.: 1 - m=10-12; 2 - "средняя" частица с m=3,45*10-12; 3 - m=10-9; 4 - m=10-6; 5 - m=10-3; 6 - m=1; 7 - m=103. Начальная температура материала выброса 1500К. |
Зависимость температуры от времени для частиц с размерами в интервале 10-4 см £ D £ 10 см (10-12 г £ m £ 103 г) показана на рис. 8. Начальная температура принята равной 1500 К, температура окружающего газа - 300 К.
2.1. Термоэмиссионный механизм электризации частиц газопепловой вулканической тучи
Как известно, с поверхности нагретого твердого тела вследствие термоэмиссии "испаряются" электроны. Термоэмиссия электронов подчиняется закону Ричардсона:
|
|
(2.5) |
где jэ — плотность термоэмиссионного тока; k = 8,6173.10-5 эВ/град — постоянная Больцмана; А0 = 120,4 А/(см2.град2) [10] — константа; АB— работа выхода материала частиц. Для материала пепловых частиц работа выхода точно не известна, но по химическому составу пеплов (хотя он и различен для разных вулканов и даже для разных извержений одного и того же вулкана, но основные компоненты SiO2, AI203, CaO, MgO [20] характерны для большинства диэлектриков) можно сделать вывод, что величина ее заключается в пределах AB» 3,5 - 4,8 эВ [10].
Для температуры частиц Т = 1500 К и AB = 4,8 эВ по формуле (2.5) получим jэ= 2,01.10-8 А/см2. Концентрацию зарядов в газе, окружающем аэрозольную частицу, можно определить, приравняв поток электронов, эмиттируемых с поверхности частиц, встречному диффузионному потоку зарядов. Поскольку электроны быстро прилипают к нейтральным молекулам газа, то все процессы в газе будут определяться концентрацией и диффузией газовых ионов. Тогда в уравнении баланса
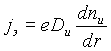 |
(2.6) |
следует использовать коэффициент диффузии ионов Dи = 0,036 см2/с [21]. Здесь nи — концентрация ионов в газе; r — координата.
Чтобы определить общий заряд, эмиттированный в газ, рассмотрим процесс эмиссии в область, окружающую одну аэрозольную частицу радиусом г0. Объем этой области, очевидно, равен 1/n.
Процесс описывается уравнением диффузии:
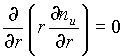 |
(2.7) |
при граничном условии:
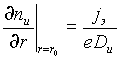 |
Решение этого уравнения:
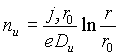 |
(2.8) |
Тогда заряд в объеме, окружающем частицу, равен:
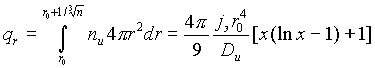 [Кл] [Кл] |
(2.9) |
где
|
|
Общий заряд QS 1 можно определить интегрированием qr no всем размерам частиц. Результаты интегрирования показаны на рис. 9. Вклад каждой частицы пропорционален величине ее поверхности, т.е. положительный заряд qэ+ (r0) частицы радиуса г0 равен:
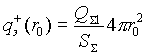 |
(2.10) |
(Поскольку в исходном уравнении (2.7) для простоты не учтено тормозящее эмиссию встречное электрическое поле, формула (2.10) дает завышенное значение заряда.)
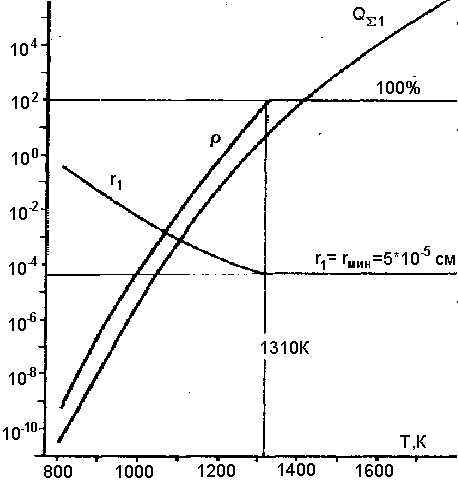 |
Рис.9. Зависимость основных параметров термоэмиссии от температуры частиц: QS1 - общий электрический заряд, Кл; Р - процент эмиттирующих частиц; r1 - минимальный радиус эмиттирующих частиц, см. |
Заметим, что при не слишком высоких температурах величина заряда qэ+ (г0) для самых мелких частиц может оказаться меньше заряда электрона. Такие частицы не могут участвовать в эмиссии, т.е. общая концентрация частиц n* и суммарная поверхность эмиттирующих частиц SS +, могут оказаться меньше n и SS , соответственно, а минимальный радиус эмиттирующих частиц r*min больше rmin=5*10-5 см. В таком случае для определения QS1 приходится пользоваться методами итерации. На рис. 9 приведены зависимости n*/n, г*min и QS 1 как функции температуры Т. Видно, что интенсивность термоэмиссии сильно меняется с температурой, а при Т<1300 К не все частицы участвуют в этом процессе. (Напомним, что оценка проведена для пеплов с максимальной работой выхода АB = 4,8 эВ.)
Время, за которое частицы эмиттируют заряд QS 1, можно оценить по формуле:
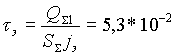 [c] [c] |
(2.11) |
Ясно, что процесс термоэмиссии электронов, даже если частицы в струе движутся со скоростью звука, закончится вблизи жерла вулкана, и наше предположение, что струя не успеет смешаться с атмосферным воздухом, вполне обоснованно (см. рис. 5). Поскольку QS 1 и jэ одинаковым образом зависят от температуры, время установления равновесия не зависит от Т, а также и от размеров частиц.
Однако, сравнивая время термоэмиссии t э ~ 5,3.10-2 с со временем остывания основной массы частиц (а это, как мы отметили выше, прежде всего мелкодисперсная фракция аэрозоля), можно заключить, что более 90% поверхности аэрозольных частиц к моменту t э уже неспособно участвовать в эмиссии, поскольку их температура оказывается ниже 1300 К. Таким образом, вычисленная величина QS1 в действительности оказывается завышенной.
Максимальные возможности термоэмиссии можно оценить, проинтегрировав по времени все то, что эмиттируют аэрозольные частицы всех размеров (отвлекаясь пока от того, куда девается эмиттированный заряд):
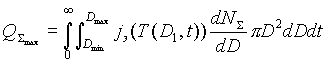 |
(2.12) |
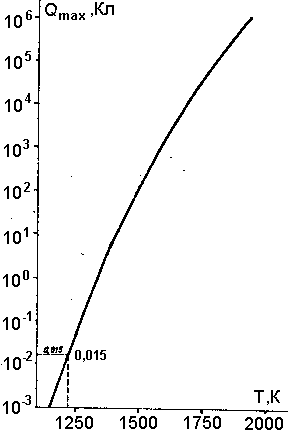
Рис. 10. Предельный заряд QSmax, обеспечиваемый термоэмиссионным механизмом электризации вулканических частиц, пунктир - минимальный заряд (0,015 Кл), необходимый для возникновения молнии длиной 50 м, и соответствующая ему минимальная температура выброса (~1220К).
Зависимость QSmax от температуры частиц показана на рис. 10. Нетрудно видеть, что, если исходная температура газопепловой смеси меньше Т » 1200 К, термоэмиссионный механизм оказывается слишком малоэффективным. (Ниже будет показано, что для образования молний длиной 50 м необходим заряд ~0,015 Кл.)
В результате процесса термоэмиссии частицы окажутся заряженными положительно, кроме самых мелких, которые останутся с нулевым зарядом. При этом отрицательный заряд сосредоточится на газовых ионах. Высокая подвижность газовых ионов (m -ион= 2,08 см2/(В.с)) [21] не позволит возникнуть хоть сколько-нибудь заметному электрическому полю (вопреки мнению, высказанному в работе [22]), поэтому молнии на этой стадии также не возникнут.
Тем не менее эта стадия термоэмиссии играет важную роль в ином смысле: аэрозольные частицы с самого начала несут на себе положительный заряд, т.е. коагуляция аэрозоля затруднена и счетная концентрация его может долгое время поддерживаться на уровне значительно более высоком, чем для незаряженных аэрозолей.
Спустя 10-2 с после остывания частиц, температура частиц, меньших 3 мкм, снижается до 1200 К, и плотность тока термоэмиссии настолько мала (jэ(T = 1200 К) = 1,2.10-12 А/см2), что равновесная концентрация газовых ионов должна быть около них на 5 — 6 порядков ниже, чем у более крупных. К этому моменту термоэмиссионный механизм зарядки качественно преобразуется. Горячие крупные частицы продолжают эмиттировать электроны, а остывшие мелкие частицы начинают эти электроны захватывать. Средняя концентрация свободных ионов в газе становится очень малой (см. приложение) по сравнению с первоначальной и баланс заряда надо оценивать исходя из других критериев, поскольку мелкие частицы составляют основную счетную массу и электрическую емкость аэрозоля. Если скорость эмиссии (определяемая плотностью тока и величиной поверхности частицы) достаточно велика, то равновесный положительный заряд q+э можно оценить следующим образом.
Можно полагать, что ион (газовая молекула, захватившая эмиттированный электрон) преодолеет кулоновское притяжение к частице, если потенциал этого притяжения порядка энергии теплового движения иона. Точность соответствия этих величин можно оценить сверху и снизу.
Очевидно, нижняя граница определяется равенством тепловой и кулоновской энергий двухатомного атмосферного иона:
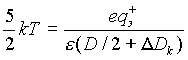 |
(2.13) |
Здесь e — диэлектрическая проницаемость воздуха; D Dk — "безопасное" расстояние, преодолев которое, ион не возвратится к частице диаметром D; Т — температура газа. Можно считать, что для всех частиц DDk» 10-5 см. Эта величина соответствует расстоянию разрыва электрического контакта между соприкасающимися частицами, когда прекращается обмен зарядами. Заметим, что в грозовых облаках при весьма слабых полях и малых зарядах расстояние разрыва уменьшается на порядок [23].
Для оценки верхней границы можно воспользоваться следующими соображениями. Газовые молекулы распределены по скоростям (и по энергиям) согласно функции Максвелла — Больцмана
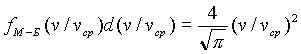 |
(2.14) |
т.е. определенная часть их имеет энергию значительно больше kТ. Оценим, какая часть всех молекул должна иметь энергию больше потенциала кулоновского взаимодействия, чтобы обеспечить отход иона на расстояние DDk= 10-5 см. Время диффузии на расстояние DDk составляет t. » (DDk)2/Dи = 2,8.10-9 с при средней скорости молекул vср » 5*104 см/с и средней длине свободного пробега l»10-5 см [21]. Молекула за это время испытает n = vср*tд./l³ 14 столкновений. Значит, искомая часть будет величиной порядка w=1/n»7,1*10-2. С другой стороны,
|
|
(2.15) |
Это соответствует v/vср = 1,88 или Е/kТ = (1,88)2 = 7/2. Таким образом, верхняя оценка дает
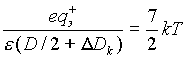 |
(2.16) |
Будем пользоваться для вычислений средним значением из двух оценок (2.13) и (2.16):
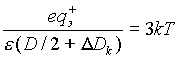 |
(2.17) |
Исходя из (2.17) найдем
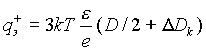 |
(2.18) |
(Полученное нами значение коэффициента при kT, равное 3, близко к значению аналогичного коэффициента в физике полупроводников, когда рассчитывается вероятность ионизации примесных атомов, где оно равно 3 — 5 [10].)
Отметим, что формула (2.18) дает | q+э | > е даже при D = 0, т.е. на второй стадии термоэмиссии частица любых размеров может эмиттировать электроны, если Т > 1200 К.
Для тех частиц, которые уже остыли и начали собирать отрицательный заряд, также существует равновесная величина этого заряда, определяемая тем же уравнением (2.17), только притяжение заменяется отталкиванием. (Здесь подразумевается, что прилипание (адгезия) отрицательных ионов или их перезарядка при соприкосновении с аэрозольной частицей имеет вероятность 100%.) Таким образом:
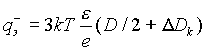 |
(2.19) |
На рис. 11 показаны зависимости q+э и qэ- от D (кривые 2 и 3) вместе с графиком функции (2.10) при Т - 1500 К (кривая 1).
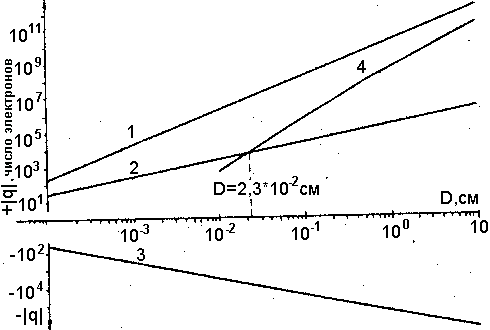
Рис. 11. Зависимость заряда аэрозольных частиц, генерируемых по термоэмиссионному механизму, от размеров частиц; 1 - первая стадия термоэмиссии (t< 5,3*10-2 c); 2, 3 - положительный и отрицательный заряды на второй стадии термоэмиссии; 4 - "сдувание" при t=9,3*10-2 c.
Заметим, что для крупных горячих частиц удаление эмиттированного отрицательного заряда возможно не только за счет тепловой энергии ионов (диффузия), но также и за счет сдувания ионов.
Электроны, эмиттированные горячей аэрозольной частицей, подхватываются обтекающим частичку потоком молекул газа. Процесс сдувания (отрыва) эмиттированных электронов будет продолжаться до тех пор, пока накапливающийся на частице положительный заряд не достигнет определенной критической величины +qk, при которой кулоновская сила притяжения электрона к частице Fкул = 4qke/D2 сравняется с силой "сдувания" электронов Fcд . Можно считать, что эмиттированные электроны прилипают при этом к молекулам газа диаметром Dмол» 3А [10] в основном к N2, O2 или парам воды. Образовавшийся при этом на поверхности частички отрицательный ион будет испытывать со стороны набегающего со скоростью v' потока силу Fсд, стремящуюся оторвать его от частицы. При Dмол <<l 0, где l 0 - длина свободного пробега, сила "сдувания" равна [5]:
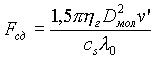 |
(2.20) |
где cs » 1 [5] - коэффициент, зависящий от свойств поверхности частичек; v' - скорость частицы относительно газа. Зная эту скорость и приравняв кулоновскую силу притяжения отрывающей силе Fсд (2.20), действующей на отрицательный ион, найдем qk — эффективный положительный заряд частицы с массой m [г]:
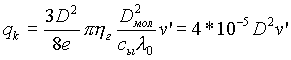 |
(2.21) |
Поскольку термоэмиссия протекает в начальные моменты выброса, когда основным процессом является не седиментация, а разгон (ускорение) частиц газовым потоком при взрыве, то относительная скорость v' в это время может быть существенно больше скорости седиментации (см. рис. 4).
Подставляя в (2.21) значение скорости, соответствующее моменту времени t = 5,3.10-2 с [см. (2.11)], можно получить зависимость qk=qk(D) (см. рис.11, кривая 4). Видно, что "сдуваемый" заряд намного меньше зарядов, определяемых формулами (2.10) и (2.18) для частиц с D<2,3.10-2 см, составляющих, как известно, основную счетную массу аэрозоля. Заметим здесь, что величина "сдуваемого" заряда на частицах с D > 2,3.10-2 см наверняка завышена, поскольку в формуле (2.21) не учтено влияние присоединенного пограничного слоя, т.е. реальная скорость обтекания частиц газом ниже, чем изображенная на графиках рис. 4.
На рис. 11 показаны величины предельных зарядов — положительного заряда горячих (эмиттирующих) частиц и отрицательного заряда холодных (неэмиттирующих) частиц. Время достижения заряда qэ+ очень резко зависит от начальной температуры аэрозольных частиц и от их размера. На рис. 12 качественно показаны характер зарядки частиц разных размеров при Т0 = 1500 К. Видно, что мелкие частицы (D~ Dmin) заряжаются отрицательно почти сразу; более крупные частицы вначале эмиттируют электроны, но после быстрого остывания могут "поглотить" электронов вдвое больше, чем эмиттировали; наконец, самые крупные во все время полета остаются достаточно горячими и всегда несут положительный заряд. Таким образом, рис. 12 отражает ход кривых перезарядки с учетом реального распределения частиц по размерам. Видно, что, начиная с некоторого размера, процесс обратной перезарядки охладившейся частицы ионами не завершается.
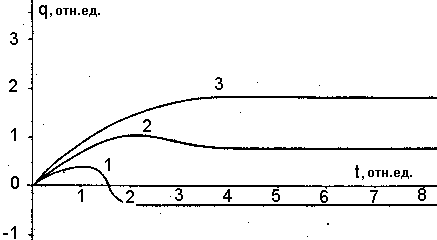
Рис. 12. Качественный ход зарядки аэрозольных частиц по термоэмиссионному механизму. Номер кривой возрастает с увеличением размера частиц.
Проверим, какова реальная ситуация. До входа в газопепловую тучу струя пролетает ~0,5 — 1 км. При движении со скоростью звука это составляет 1,5 — 3 с. По данным рис. 8 нетрудно видеть, что к этому моменту перестанут эмиттировать (Т < 1200 К) частицы с D < 200 мкм. Суммарная электрическая емкость этих частиц составляет >99,99% общей электрической емкости. Таким образом, холодные частицы могут поглотить заряд во много раз больше того, что могут эмиттировать горячие; следовательно, и процесс перезарядки, и величина максимально достижимого суммарного разделенного заряда ограничены только возможностями эмиссии, а не адсорбцией ионов на частицах.
Оценим количественные характеристики перезарядки аэрозольных частиц. Поскольку электрическая емкость холодных частиц превышает емкость эмиттирующих горячих частиц уже через ~0,01 с с момента выброса, то концентрацию ионов в газе мы можем считать близкой к нулю (функция этих ионов сводится только к переносу заряда с одних частиц на другие). Ясно также, что большинство холодных частиц вследствие этого не сможет зарядиться до qэ-. Более того, подавляющее большинство крупных частиц, даже перестав эмиттировать после охлаждения до Т < 1200 К, как показано на рис. 12, останутся положительно заряженными, так как более обильная мелкодисперсная фракция просто не пропустит к остывшим крупным частицам нужное число ионов для компенсации ранее эмиттированного заряда. Это позволяет нам воспользоваться следующим приближением. Будем считать, что все эмиттированные электроны, несущие суммарный заряд Q-S2,осядут на мелкодисперсных частицах, зарядив каждую частичку всего одним избыточным электроном.
Легко показать, что
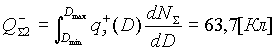 |
(2.22) |
Распределение заряда частиц по размерам qэ2 после полного высаживания на них заряда -|QS 2| рассчитывается по соотношению:
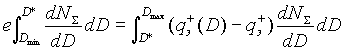 |
(2.23) |
Здесь D* — размер частиц, при котором сравниваются заряды; q*э -заряд, рассчитанный по (2.18) и соответствующий D*. Расчеты дают, что D* = 3,7.10-4 см, a qэ* - 1,68.10-17 Кл. Заметим, что формула (2.23) описывает процесс, когда все частицы эмиттировали заряд QS2, затем все одновременно перестали эмиттировать и с равной вероятностью стали захватывать заряд из газа. Можно рассмотреть другой крайний случай, когда после эмиссии заряда Q-S2 обратный захват заряда происходит только на остывших частицах. В этом случае второй член -q*э в правой части уравнения (2.23) отсутствует:
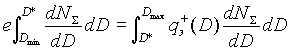 |
(2.24) |
Расчеты по такой формуле дают D*= 6,4.10-4 см, a q*э = 2,87.10-17 Кл. (Реальная ситуация находится где-то между этими крайними возможностями, и мы приняли D* = 5.10-4 см.) Во втором случае кривая распределения заряда имеет разрыв (минимальный положительный заряд аэрозольной частицы равен 2,87.10-17 Кл или 178 электронов, а все частицы размером меньше D* - 6,4.10-4 см несут на себе по одному электрону), который является следствием искусственного разграничения процессов эмиссии и обратного осаждения электронов на аэрозольных частицах.
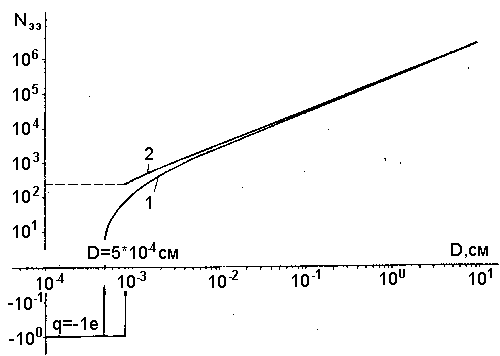
Рис. 13. Зависимость равновесного числа эмиттированных электронов Nээ от размера аэрозольной частицы. 1, 2 - расчет по формулам (2.23) и (2.24), соответственно, для момента времени через 10 с после взрыва.
Результирующее распределение заряда по размерам (через 10 с после взрыва) для обоих рассмотренных выше случаев показано на рис. 13. К этому времени частицы всех размеров достигнут равновесного заряда (крупные и горячие — в силу того, что на них уже есть заряд q*э, "запрещающий" дальнейшую эмиссию, а остывшие — в силу того, что им нечем больше заряжаться). Интегрирование кривой q (D) (см. рис. 13) с учетом количественных характеристик выброса (см. разд. 1) показывает, что заряд каждого знака составляет в первом случае (формула (2.23)) 1,36 Кл, во втором - 1,45 Кл. Сравнив полный эмиттированный заряд Q-S 2 = 63,7 Кл [см. (2.22)] с разделенным зарядом, оставшимся после высаживания (~ 1,4 Кл), можно видеть, что лишь малая доля эмиттированного заряда (~2%) участвует в процессах макроскопического масштаба (образования молний).
Интересно, что заряд этот в нашем приближении почти не зависит от начальной температуры Т0 материала выброса при условии, что Т0 > 1400 К.
Задачу термоэмиссионной перезарядки вулканического аэрозоля можно решить на ЭВМ. Это было выполнено при следующих предположениях:
1) распределение частиц по размерам описывается выражением (1.5);
2) выброс — разовый, основные параметры выброса перечислены в разд. 1;
3) в кинетическом уравнении термоэмиссионной перезарядки учтены только процессы эмиссии электронов и одновременного обратного высаживания эмиттированного заряда на аэрозольных частицах, величина свободного заряда в газе пренебрежимо мала;
4) вероятность высаживания электрона на частице зависит только от площади поверхности этой частицы;
5) перезарядка вследствие столкновений частиц между собой не учитывается.
|
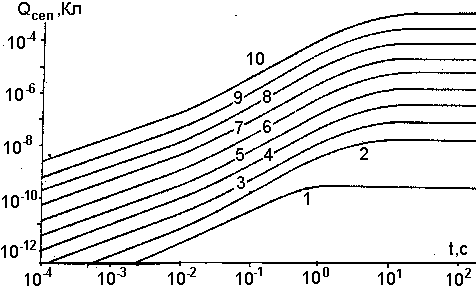
Рис. 14. Зависимость разделения заряда вследствие термоэмиссии шлакопепловых частиц с различной работой выхода Ав от времени, эВ: 1 - 4,8; 2 - 4,65; 3 - 4,5; 4 - 4,36; 5 - 4,21; 6 - 4,07; 7 - 3,93; 8 - 3,64; 9 - 3,79; 10 - 3,5. Начальная температура пепловых частиц 1500К, масса аэрозольных частиц от 10-12 до 103 г.
|
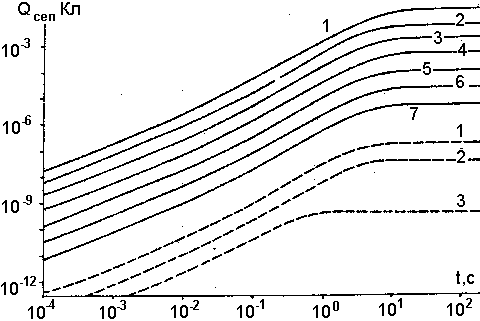 |
Рис. 15. Зависимость изменения разделенного заряда от времени при термоэмиссионном механизме перезарядки вулканических частиц и различной начальной температуре, Т0, К: 1 - 1600; 2 - 1550; 3 - 1500; 4 - 1450; 5 - 1400; 6 - 1350; 7 - 1300. Сплошные линии - Ав = 3,5 эВ; пунктир - Ав = 4,8 эВ. Масса аэрозольных частиц от 10-12 до 103 г. |
Результаты расчета представлены на рис. 14 и 15, на которых показаны изменения величины разделенного заряда Qсеп в зависимости от времени (параметром является работа выхода пепловых частиц).
Интересно отметить, что процесс эмиссионной перезарядки обрывается во времени довольно резко, причем момент прекращения процесса практически не зависит от величины работы выхода (во всяком случае, для тех комбинаций Ав и Т0, когда эмиттированный заряд имеет существенную для нашей задачи величину). Однако количественные характеристики процесса сильно зависят и от Т0, и от АВ.
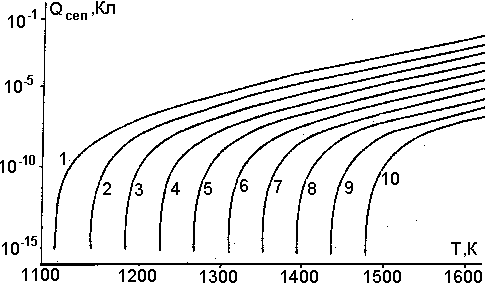 |
Рис. 16. Зависимость величины заряда, разделенного к моменту окончания термоэмиссии, от начальной температуры шлакопепловых частиц с различной работой выхода Ав, эВ: 1 - 3,5; 2 - 3,64; 3 - 3,79; 4 - 3,93; 5 - 4,07; 6 - 4,21; 7 - 4,36; 8 - 4,5; 9 - 4,65; 10 - 4,8. |
На рис. 16 построена зависимость суммарного разделенного заряда Qсеп (спустя ~10 с после выброса) от начальной температуры То для пеплов с различной работой выхода. Видно, что для "горячих" аэрозолей (когда выполняется условие Т0/АВ > 315) логарифм суммарного заряда линейно зависит от АВ, температурная зависимость его приближенно выражается соотношением
| (2.25) |
Пороговая температура Тпор, ниже которой вклад термозмиссионного механизма становится пренебрежимо малым, в первом приближении определяется соотношением:
| (2.26) |
Количественные характеристики термоэмиссионного механизма, полученные более строгим машинным расчетом, оказываются существенно скромнее, чем давали наши грубые оценки.
Дальнейшие процессы перезарядки связаны с седиментацией частиц, несущих на себе электрический заряд, столкновениями и перезарядкой. В нашем распоряжении имеются почти все данные, необходимые для расчета этой стадии процесса. Однако полезно вспомнить, что на этой стадии, когда аэрозоль уже охлажден, эмиссия прекратилась и имеет лишь "историческое" значение для последующей перезарядки, основная роль принадлежит уже не термоэмиссии, так что необходим учет новых факторов, о которых будет сказано ниже.
В заключение настоящего раздела еще раз кратко обрисуем трансформацию процесса термоэмиссии во времени. В момент выброса все частицы, будучи горячими, эмиттируют достаточное количество эпектронов. При этом за время t £ 10~4 с достигается равновесие между положительно заряженной твердой фазой и отрицательно заряженной газовой плазмой выброса. Однако уже спустя 10-3 с мелкодисперсная фракция аэрозоля остывает и захватывает весь эмиттированный заряд. Начинается вторая стадия термоэмиссионного механизма. Крупные, не успевшие остыть частицы продолжают эмиттировать электроны, которые тут же захватываются холодной "мелочью". Поскольку, суммарная электрическая емкость остывшей фракции в облаке на несколько порядков больше емкости горячих частиц, все еще продолжающих эмиттировать электроны, то процесс здесь ограничен только возможностями именно этих эмиттирующих частичек. Эта стадия длится 2 — 10 с.
И, наконец, почти одновременно со второй стадией начинается третья — стадия компенсации разделенных зарядов при седиментации заряженных частиц.
2.2. Термоэлектрический механизм электризации частиц вулканического аэрозоля
Рассмотрим теперь термоэлектрический механизм образования и разделения зарядов в газопепловой вулканической туче. Вкратце он сводится к тому, что при соприкосновении двух аэрозольных частиц разной температуры электрическое состояние их может изменяться за счет разности работ выхода. Температурный коэффициент работы выхода для материала частиц будем считать равным: dAB/dT = -1,5.10-3 эВ/град [10].
Посмотрим, что произойдет при однократном столкновении двух нейтральных частиц размерами D1= 1 мкм и D2 = 100 мкм, большая из которых имеет температуру всего на D Т = 10 К выше меньшей. (На рис. 8 это соответствует времени через 40 с после выброса). Значению DТ = 10 К соответствует величина термоэ.д.с. DU = 0,015 В, т.е. при соприкосновении таких частиц возникающая разность потенциалов будет исчезать за счет перетекания заряда Dq — электроны с крупной горячей частицы перейдут на мелкую. Емкость мелкой частицы C1= 5.10-5 см = 5.6.10-17 Ф, большей С2 = 5,6.10-15 Ф. Так как потенциалы соударяющихся частиц при соприкосновении сравниваются, то:
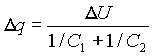 |
(2.27) |
откуда видно, что изменение заряда D q определяется емкостью меньшей частицы C1 и равно D q=D U*C1 = 8,33*10-19 Кл =2,5.10-9 эл. ст. ед. @ 5 электронам.
Если кулоновская сила притяжения заряженных частиц больше силы сдувания, то частицы не разлетятся до тех пор, пока меньшая частица не прогреется до соответствующей температуры. Величину силы сдувания можно определить исходя из вязкой силы Стокса (1.7) FB = 3p h vD, где D = D1— диаметр меньшей (сдуваемой) частицы; v = v1,2 — разница скоростей оседания частиц, v1,2 ~ v2 =30 см/с, так как V1 = 7.10-3 см/с << v2. В данном примере сила сдувания FB = 3ph vD1 = 4,7.10-6 дин значительно превышает кулоновскую силу Fкул = D q2/r2T = 1,6*10-13 дин [rт = 0,5(D1 + D2)], а следовательно, такое столкновение действительно приведет к переходу 5 электронов с большей частицы на меньшую. Заметим, что практически для всех сталкивающихся частиц, представляющих интерес с точки зрения термоэлектрической перезарядки, кулоновские силы значительно слабее сил сдувания, так что в дальнейшем мы на этом вопросе останавливаться не будем. Время электрического контакта частиц равно tc ³ 0,1D2/v2 - 3,4.10-5 с. Время растекания заряда по объему частицы (независимо от ее размеров) равно tp = e ese, где ee и s e — диэлектрическая проницаемость и электропроводность материала аэрозольных частиц. Для горячих частиц se = 0,065 Ом-1.м-1, для холодных se ~8,3.10-7 Ом-1 .м-1 [24], a ee. ~ 5. Таким образом, для горячих частиц tp ~ 10-9 с, для частиц комнатной температуры tp ~ 10-4 с. Это значит, что для горячих частиц обмен зарядами будет происходить в полной мере, в то время как для остывших время соприкосновения недостаточно для полной передачи заряда. Граничная температура Т = 400 ¸ 500 К. Заметим, что эта температура относится к большей по размерам (т.е. более горячей) из сталкивающихся частиц, поскольку именно она определяет эффективное расстояние < r> между зарядами.
Каждое следующее столкновение 100-мкм частицы с такими же нейтральными микронными частицами (при той же разнице температур) будет также приводить к ее подзарядке до тех пор, пока большая частица не выйдет из облака или пока ее заряд, определяемый ее емкостью, не достигнет значения qгр = D q(С2/C1) = 2,5.10-7эл. ст. ед. = 520 электронов. Зарядка большей частицы идет по экспоненциальному закону. Для того чтобы горячая частица зарядилась до ~0,7 qгр, ей необходимо испытать ~100 столкновений. (Для холодных (<400К) частиц, где допустим переход, по-видимому, только одного электрона, число столкновений увеличивается до ~500.) Зная частоту столкновений частиц в аэрозольном облаке (см. рис. 6), нетрудно оценить, что для достижения равновесного заряда в данном случае требуется ~10-3 с.
Сопоставляя скорости охлаждения частиц различного размера и дисперсный состав аэрозоля, нетрудно установить, что процесс термоэлектрической зарядки почти полностью определяется столкновениями частиц крупнее 5-10 мкм с микронными частицами, имеющими температуру окружающего воздуха.
Такое упрощение становится возможным по следующим причинам:
— охлаждение микронных частиц заканчивается через 0,01 — 0,1 с, в то время как более крупные частицы сохраняют тепло значительно дольше;
— остывшие частицы малого размера составляют основную счетную массу аэрозоля, частота столкновений любых более крупных частиц с ними значительно выше, чем между собой (см. рис. 7);
— электрическая емкость остывшей мелкодисперсной фракции значительно выше, чем неостывшей, поэтому перезарядка определяется только тем, сколько заряда могут отдать нагретые частицы, а не тем, сколько их может принять масса холодных мелких частиц.
Это упрощение позволяет получить количественные характеристики термоэлектрического механизма электризации. Если положить, что время релаксации заряда частицы меньше времени остывания, то тогда равновесный положительный заряд каждой еще не остывшей частицы в каждый данный момент времени однозначно определяется ее размером (т.е. электрической емкостью) и температурой. Поскольку наибольшая скорость остывания наблюдается в начальные моменты времени, ясно, что последнее предположение выполняется с достаточной степенью точности лишь спустя некоторое время от момента взрыва. Однако это время (порядка 0,1 — 1 с) значительно меньше длительности рассматриваемых процессов электризации, так что равновесное распределение положительного заряда по размерам частиц представляет несомненный практический интерес.
Отрицательный заряд распределяется по мелким остывшим частицам. Сколько лишних электронов окажется на каждой мелкой частице — это зависит не только от ее размера, но также и от того, какая частица ей эти электроны передала. Однако и здесь задача легко упрощается. Поскольку скорость осаждения микронных отрицательно заряженных частиц (см. рис. 3,а) очень мала и слабо зависит от величины заряда, то само распределение этого заряда по мелким частицам совершенно несущественно, и без большой погрешности можно считать отрицательный заряд "подвешенным" в газе вместе с мельчайшими аэрозольными и "осаждающимся" вместе с этими частицами со средней скоростью седиментации 6,1.10-2 см/с. (Эта скорость соответствует "средней" частице облака с mср = 3.45.10-11 г.) Единственное условие, выполнения которого требует последнее упрощение, это чтобы суммарная электрическая емкость остывшей части аэрозоля была значительно больше, чем его горячей части.
Оценки показывают, что спустя секунду после взрыва это условие выполняется с запасом в три порядка величины, так что уже в верхней части струи (см. рис. 5) термоэлектрический механизм можно описывать, пользуясь нашими упрощениями.
Исходя из данных рис. 8, можно рассчитать кинетику изменения суммарного равновесного разделенного заряда аэрозольных частиц:
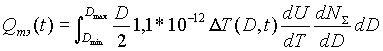 [Кл] [Кл] |
(2.28) |
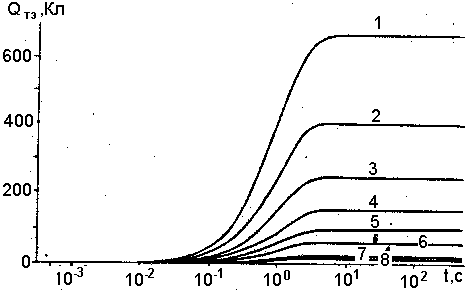
Рис. 17. Зависимость суммарного равновесного разделенного заряда Qтэ в вулканическом аэрозоле от времени при термоэлектрическом механизме перезарядки. Минимальная масса частиц mmin, г: 1 - 10-12; 2 - 1,78*10-12; 3 - 3,16*10-12; 4 - 5,62*10-12; 5 - 10-11; 6 - 1,78*10-11; 7 - 3,16*10-11; 8 - 5,62*10-11. Начальная температура аэрозоля 1500К.
Результат численного интегрирования (2.28) представлен на рис. 17 в виде семейства кривых, каждая из которых соответствует своему значению Dmin — минимального размера пепловых частиц (поскольку именно этот фактор сильнее всего влияет на конечный результат) . Следует ожидать, что электрическое поле в облаке меняет процесс макроскопического разделения заряда. Однако расчет показал, что максимальное изменение величины разделенного в облаке заряда в поле ~4 кВ/см составляет всего ~ 15% и наблюдается для аэрозоля, содержащего наиболее мелкодисперсную фракцию (m ~10-12г).
Как и для термоэмиссионного механизма [см. (2.25)], здесь удается представить зависимость равновесного разделенного заряда Qтэ (Кл) от Dmin и Т0 (К) в виде эмпирической формулы:
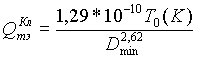 |
(2.29) |
Из (2.28) и (2.29) видно, что абсолютная величина Qтэ зависит от начальной температуры материала выброса линейно, т.е. гораздо слабее, чем при термоэмиссионном механизме электризации {см. (2.5) и (2.12)). Казалось бы, это должно растянуть во времени сам процесс перезарядки, однако сравнение рис. 14 и 17 показывает, что термоэлектрический механизм основную "работу" совершает в первые 1 — 2 с, после чего разделенный заряд как бы замораживается и обратная перезарядка не оказывает влияния на конечный результат.
Кажущаяся парадоксальность полученного результата объясняется просто. Физика термоэмиссионного механизма перезарядки в нашей модели никак не зависит от счетной концентрации аэрозоля, а только от процесса охлаждения самих аэрозольных частиц, поэтому время действия термоэмиссии не зависит от характера расширения облака. В то же время термоэлектрический механизм работает эффективно только при очень высокой счетной концентрации аэрозоля, т.е. в начальной стадии выброса. Тем не менее, времена действия обоих механизмов должны иметь один и тот же порядок, поскольку в их основе заложен общий принцип различия температур разных фракций аэрозоля.
Более подробный анализ кинетики термоэлектрической перезарядки показал, что разделенный заряд продолжает увеличиваться даже при t » 103 с, т.е. рекомбинация сталкивающихся частиц с разноименным зарядом является гораздо менее эффективным процессом, чем продолжающаяся "подзарядка" за счет оставшейся разности температур.
И, наконец, сравнение абсолютных величин термоэмиссионного и термоэлектрического механизмов показало, что первый из них может являться основным лишь при извержениях с высокой начальной температурой пирокластического материала и малых энергиях выбросов (т.е. сравнительно больших Dmin). В связи с этим расчет третьей стадии термоэмиссионного механизма — обратной перезарядки при седиментации (см. подразд. 2.1} не имеет практической ценности и мы его не приводим.
Вообще говоря, термоэлектрический механизм электризации и разделения зарядов по своему действию шире, чем термоэмиссионный. Он функционирует для твердых аэрозольных частиц любой температуры (лишь бы она хотя бы на 5 — 10 К отличалась для частиц разного размера) и с любыми электрическими свойствами, а значит, и для электризации снеговых и ледяных частиц, и для пепловых вулканических туч , и для любых смесей аэрозольных частиц с разной работой выхода. Кроме того, он пригоден и для объяснения электризации капелек водяного тумана, так как жидкие незаряженные капельки испаряются тем быстрее, чем меньше их размер, а значит, при столкновении нейтральных капелек разного размера они имеют различную температуру. Другими словами, у жидкой маленькой капельки имеется только два пути: либо полностью испариться, либо отобрать электрон у капли большего размера и тем самым стабилизироваться (как в камере Вильсона).
2.3. Другие механизмы электризации частиц пепла
Рассмотрим коротко другие возможные механизмы электризации вулканического аэрозоля, часто упоминаемые в литературе, например пьезоэлектризацию и механизмы, рассмотренные в статье [4] и книге [25], а именно: трение шлакопепловых частиц о стенки канала жерла при движении газопепловой струи наружу; взаимное трение и столкновения частиц пепла; баллоэлектрический эффект (явление электризации мельчайших частиц лавы при взрывном дроблении ее на начальной стадии взрыва).
Пьезоэлектрический механизм. Первое и наиболее важное условие работы этого механизма — наличие в составе пепла пьезоэлектрического материала. Большое процентное содержание SiО2 еще не означает, что в материале пепла присутствует пьезокварц. Даже если материал выброса целиком состоял бы из двуокиси кремния, то все равно высокие скорости остывания (см. рис. 8) делают весьма маловероятным образование правильных кристаллов кварца с упорядоченным расположением больших массивов молекул окиси кремния именно в решетку кварца. Во всяком случае, если этот процесс и имел бы место, то только в крупных шлаковых частицах (D ³10мм), так как большая часть материала застывает в аморфном или мелкокристаллическом виде. Правда, это привело бы к наличию по крайней мере двух разных типов частиц: крупных пьезоэлектрических кристаллов и мелких частиц, не обладающих пьезоэлектрическими свойствами. Однако и это предположение мало что дает. Элементарный акт пьезоэлектрической зарядки, по-видимому, можно представить себе так: две частицы сталкиваются, от удара за счет изменения дипольных моментов молекул пьезокристалла на гранях последнего возникает разность потенциалов, и заряд с той грани, к которой прикоснулась ударяющаяся частица, на нее перетекает. Однако знак пьезоэ.д.с. при ударе зависит от места на пьезокристалле, в которое ударилась встречная частица. В первом приближении соотношение площадей поверхности пьезочастицы, на которых знаки э.д.с. положительный и отрицательный, равно 1:1, т.е. вероятность зарядки налетающей частицы положительным и отрицательным электричеством совершенно одинакова (независимо от материала, скорости и размеров частиц). Таким образом, даже если в туче и будут реализованы все перечисленные предположения, то все равно заряд на частицах любого фиксированного размера будет распределен статистически одинаково (при среднем заряде, равном нулю). Для того чтобы средний заряд отличался от нуля, нужно потребовать выполнения еще одного довольно экзотического условия: пьезокристаллы должны двигаться в туче ориентированно, вперед всегда одной гранью. Поскольку факторов, стабилизирующих полет пепловых частиц, не обнаружено, то приходится сделать вывод, что пьезоэлектричество никакого вклада в зарядку вулканической шлакопепловой тучи не вносит.
По тем же причинам (отсутствие асимметрии в распределении заряда) следует отвергнуть и пироэлектрический механизм электризации, когда речь также сводится к полярной зарядке пироэлектрического кристалла при охлаждении с последующим разламыванием кристалла и разделением заряда.
Электризация трением. Во многих публикациях (см, библиографию в [3], книгу [25] или работу [26]) в качестве одного из механизмов зарядки называют трение. По-видимому, небесполезно напомнить, что трибоэлектричество, или электризация трением, в основе своей имеет тот же физический процесс, что и рассмотренный выше термоэлектрический механизм — переход электронов при соприкосновении тел с различной работой выхода. При этом различие работ выхода может быть вызвано любыми причинами: разными температурой, химическим составом, плотностью и т.д. Однако в ряде случаев трибоэлектрический механизм привлекается, по нашему мнению, необоснованно. Один из примеров — трение частиц о стенки канала жерла. Если предположить, что начальный объем камеры жерла, в которой происходят взрывы, составляет 1000 м3 [4], то площадь поверхности стенок жерла (в зависимости от его формы) равна 200 — 400 м2. Если сравнить эту величину с суммарной площадью поверхности аэрозольных частиц (S£ - 8,2.107 м2), то станет ясным, что лишь ничтожной части этих частиц хоть раз придется соприкоснуться со стенкой жерла. Кроме того, даже если при таком соприкосновении и происходит обмен зарядами между материалом выброса и стенкой, то процесс этот ограничен электропроводностью материала стенки. Удельное электросопротивление материала при температуре затвердевания лавы r = 15 Ом.м [24], а ее потенциал V по отношению к материалу выброса должен быть близок к нулю, иначе зарядка пойдет в другую сторону, т.е. должно выполняться условие V < 1 В. Если полагать, что электропроводный горячий канал имеет диаметр » 20 м и эффективную длину ~500 м, то сопротивление такого канала Rк=r l/s » 25 Ом и ток, текущий по каналу, Iк=V/RK » 4.10-2 А. Тогда за время выброса tв ~ 10-2 с будет разделен заряд Q=Iк*tв» 4.10-4 Кл. Это значительно меньше, чем заряды, возникающие благодаря процессам внутри газопелловой смеси.
Предположение, что в трении о стенки жерла существенны лишь частицы с размерами порядка шероховатости канала, т.е. сравнительно крупные с D= 0,5 ¸ 10 мм [4], еще больше уменьшает величину разделенного заряда, поскольку суммарная электрическая емкость крупнодисперсной фракции аэрозоля незначительна (см. рис. 3).
Наконец, следует подчеркнуть, что столкновения частиц пепла и их электризация происходят в основном не потому, что смешиваются и трутся друг о друга струи, несущие эти частицы [4], а из-за разности скоростей седиментации частиц. Поэтому трение струй никак нельзя считать ответственной за зарядку частиц пепла. Тем не менее, такие явления, как турбулентность и вообще движение воздушных масс [27, 28] (в том числе и ламинарное), — весьма важный фактор при разделении заряда и возникновении молний, поскольку относительное перемещение отдельных макроскопических объемов облака способно сблизить далекие области с большой разностью потенциалов до расстояний, когда эта разность потенциалов станет достаточной для пробоя. Весьма существенно здесь то, что скорость перемещения макроскопических объемов облака значительно выше средней скорости седиментации шлакопепловых частиц в этом объеме. Иначе говоря, заряд, возникший в результате седиментационного разделения, оказывается как бы встроенным, "привязанным" к быстро перемещающемуся газовому объему.
Баллоэлектрический механизм, т.е. электризация частиц лавы при дроблении. Можно показать, что этот эффект становится существенным лишь при субмикронных размерах частиц, меньших 0,001 мкм. Однако расчет (см. разд. 1) показывает, что такие частицы в заметном количестве могут появляться лишь при вулканических взрывах большой энергии (>1020 эрг), а поскольку молнии наблюдаются и в облаках менее мощных взрывов, то нет оснований для привлечения этого механизма (кстати, очень плохо изученного). Естественное увеличение электрической активности в вулканическом облаке по мере роста энергии взрыва вполне можно объяснить в рамках рассмотренных выше термоэмиссионного и термоэлектрического механизмов электризации частиц пепла.
|
"На третий день, при наступлении утра, были громы и молнии, и густое облако над горою, и трубный звук весьма сильный... и восходил от нее дым, как дым из печи, и вся гора сильно колебалась. И звук трубный становился сильнее и сильнее". Библия, Исход, гл. 19. |
3. КИНЕТИКА РАЗДЕЛЕНИЯ ЗАРЯДА И ОБРАЗОВАНИЕ МОЛНИЙ В ВУЛКАНИЧЕСКИХ ТУЧАХ
Молния, т.е. электрический заряд в газовой среде, возникает тогда, когда в каком-либо макроскопическом объеме (размером не менее нескольких метров) достигается напряженность электрического поля, равная пробойной. По-видимому, аналогия электрических процессов в грозовых и вулканических тучах достаточно глубока. Это дает возможность воспользоваться некоторыми количественными характеристиками процессов в грозовых облаках и с их помощью оценить ряд параметров электрических разрядов в вулканических тучах.
Вначале напомним некоторые характеристики грозового электричества, надежно подтвержденные многочисленными экспериментальными измерениями (см. [14], с. 256):
Средняя длина грозовой молнии — 4 км.
Средний заряд, разряжаемый молнией — 25 Кл.
Максимально измеренная напряженность электрического поля в грозовых облаках (пробивная напряженность) — 4 кВ/см.
Заряд, образуемый в грозовой туче за время между двумя последовательными молниями, на два порядка больше, чем заряд, переносимый молнией.
Первые две величины позволяют оценить среднее электрическое поле в разрядном промежутке в момент возникновения молнии. Если положить, что молния длиной 4 км возникает между двумя заряженными сферическими областями, радиус каждой из которых равен 2 км, то нетрудно вычислить, что среднее поле в грозовой туче равно 300 — 400 В/см, т.е. на порядок ниже пробивного. Чем вызвано такое резкое различие средней и пробивной напряженности поля? Причина в том, что молния развивается сначала в малой области, в которой вследствие флуктуации заряда достигнуто пробивное поле: "подожженный" таким образом заряд развивается дальше путем последовательного пробоя на одном или обоих концах "металлизированного" разрядного канала (так называемый "стримерный" механизм пробоя).
По своим электрическим характеристикам холодный газ с заряженными каплями воды, по-видимому, не слишком сильно отличается от холодного газа с заряженными частицами пепла. Это дает основание считать, что величины предельной и средней напряженности электрического поля в обоих видах туч одинаковы (во всяком случае, мы не располагаем данными, противоречащими этому утверждению). Правда, такое равенство представляется естественным только при полном размерном подобии процессов разделения заряда и турбулентного перемешивания отдельных объемов облака. В грозовой туче при длине молнии 4 км размер отдельного клуба облака (или отдельной "флуктуации") имеет величину 100 — 300 м, т.е. на длине 4 км укладывается от 15 до 40 таких "флуктуации". В вулканической туче значительно "теснее". Только в зоне III ветрового сноса (см. рис. 5) масштабы явлений приближаются к грозовым (молнии длиной до 1 — 2 км [3], клубы и струи в сотни метров). В зонах же I и II характерные размеры клубов составляют 0,1 — 0,3 размера всей области, а значит, среднее поле должно значительно меньше отличаться от максимального. Струю у жерла мы не рассматриваем, поскольку молнии в ней не рождаются, хотя она в силу высокой электропроводности раскаленного газа и является "громоотводом" для многих молний, родившихся в области I, Масштабная оценка позволяет предположить, что среднее электрическое поле в зонах I и II при интенсивном образовании молний составляет около 1 к В/см.
Теперь оценим величину разделенного заряда в зависимости от длины молнии. Пусть молния длиной L0 разряжает два объема, каждый из которых имеет характерный размер (диаметр) D0~L0. Тогда при среднем поле Е = 1 кВ/см нетрудно получить, что заряд Q0 каждого объема равен:
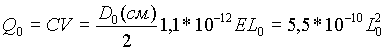 [Кл] [Кл] |
(3.1) |
Таким образом, для молний длиной 200 м требуется заряд 0,22 Кл, в то время как для 10-метровой молнии - всего 5,5.10-4 Кл.
Очевидно, заряд Q0, разряжаемый при длине молнии L0, разумно отнести к шару диаметром 2L0, т.е. к объему V0 = p /6. (2L0)3 » 4L3o. Тогда плотность заряда равна
|
|
(3.2) |
Не вдаваясь в подробности распределения заряда в макроскопическом масштабе, ограничимся оценками характеристик электрической активности в вулканической шлакопепловой туче, используя аналогию с процессами в грозовых облаках [1, 14]. Основания для такой аналогии есть, так как в водяном тумане, как правило, имеет место направленная электризация капель, а знак и величина заряда капли зависят от ее размера. Механизмы же турбулентного перемешивания [27] в обоих случаях одинаковы (в нашем случае во всех областях, кроме, может быть, струи в непосредственной близости от жерла) и различаются лишь временными характеристиками.
Оценим сначала, какую долю разделенного заряда переносят молнии в вулканической туче. Величина 0,01, характерная для грозовых туч, может быть принята в качестве нижнего предела. Известно, что грозовые капли за свою историю успевают несколько раз изменить не только величину, но и знак заряда, что связано с физическими особенностями поведения воды в атмосфере (испарение, замерзание, дробление и т.д.) [29]. Кстати, это в известной мере обусловливает и величину несоответствия среднего и пробивного полей в грозовой туче [30]. Шлакопепловые частицы в вулканическом облаке не испаряются, не дробятся (во всяком случае, это справедливо для мелких частиц, определяющих электризацию), температура и электризация их меняются монотонно, а направленность электризации (везде, кроме, может быть, струи) постоянна. Это значит, что статистический разброс заряда и электрического поля в нашем случае будет существенно меньше, меньше будут и "бесполезные" потери заряда. Единственный механизм потерь заряда — компенсация при столкновении разноименно заряженных частиц — полностью учитывается в подразделе 2.2, где рассмотрены термоэлектрические явления. По-видимому, рассеянный заряд, не "выразившийся" в молниях, можно оценить так. Если средняя длина молнии составляет 0,3 диаметра облака, то можно предположить, что в остальном объеме облака, не захваченном молнией, концентрация заряда приблизительно .вдвое меньше, чем в разряжающемся объеме. Тогда доля накопленного заряда, переносимого молниями, составляет ~0,05. Однако в действительности эта цифра может оказаться выше, поскольку оставшийся заряд за время между молниями не успевает исчезнуть, скомпенсироваться и будет участвовать в формировании следующих молний. Таким образом, "коэффициент использования заряда" в вулканической туче зависит от двух величин: длины молний (точнее, от отношения этой длины к размеру области вулканического облака, в котором идут молнии) и интервала между последовательными разрядами.
В качестве верхнего предела "коэффициента использования заряда" разумно принять величину ~0,05 - 0,1, причем этот верхний предел выше для зон I и II, в зоне же ветрового сноса условия, по-видимому, близки к грозовым.
Таким образом, можно теперь сформулировать оценочные условия возникновения молний в газопепловой вулканической туче:
1) среднее электрическое поле в разрядном промежутке должно достичь в зонах I и II значения 1 кВ/см и в зоне III 300 — 400 В/см;
2) заряд Q0 в кулонах, необходимый для возникновения молнии длиной L0 (см), равен Q0 = 5,5.10-10 • L20. При этом средняя плотность разделенного заряда составляет r (Кл/см3) = 1,4.10-10 Lo-1;
3) общий разделенный заряд в зонах I и II вулканического облака в ~10 — 20 раз больше заряда, переносимого молниями; в зоне III эта цифра возрастает до ~100;
4) средняя длина молний ~0,3 диаметра области (клубящегося сгустка), в которой она наблюдается. (Исключение составляют короткие молнии длиной 8 — 10 м в приземных слоях, накрытых вулканической тучей.)
Посмотрим теперь, насколько эти цифры соответствуют полученным результатам. Собственно, нам нужны лишь итоговые графики рис. 14 и 17, а точнее, рис. 17, поскольку уже установлено, что термоэлектрический механизм на несколько порядков эффективнее, чем термоэмиссионный.
Из формулы (3.2) можно вывести количественный критерий возникновения молний в масштабе всего облака. Учитывая "коэффициент использования заряда", определенный выше, получим: для областей I и II:
| (3.3) |
для зоны ветрового сноса:
| (3.4) |
или в виде величин суммарного разделенного заряда и полного объема облака соответственно:
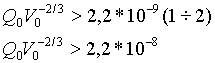 |
(3.5) (3.6) |
На рис. 18 для термоэлектрического механизма электризации построена зависимость плотности объемного заряда r = Qo/V0 от времени. Там же приведены пороговые линии для возникновения молний фиксированной длины и "глобальных" молний в масштабе всего облака. Видно, что критерий образования крупномасштабных молний занижен.
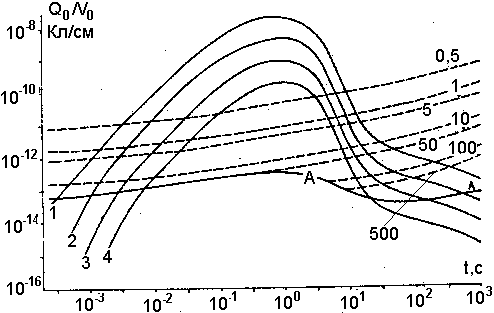
Рис. 18. Зависимость средней плотности объемного заряда в вулканическом облаке от времени. Минимальная масса аэрозольных частиц mmin, г.: 1 - 10-12; 2 - 5,62*10-12; 3 - 3,16*10-11; 4 - 1,78*10-10. Кривая А отражает критерий возникновения "глобальных" молний, пунктирные линии - критерий возникновения молний фиксированного размера, величина которого в метрах указана над линиями (с учетом формул (3.3), (3.4))
Заметим сразу же, что рис. 18 отражает только возможность возникновения молний, но не реализацию этой возможности. Однако он позволяет выявить некоторые качественные особенности кинетики образования молний. А именно — в первую очередь появляются условия для возникновения разряда в масштабе всего облака и лишь несколько позже для возникновения молний более мелкого масштаба. Когда в какой-то момент t0 реализуется молния определенного масштаба, соответствующая кривая на рис. 18 с этого момента должна быть смещена вниз на величину, соответствующую заряду, перенесенному молнией. Таким образом, каждая молния изменяет вероятность дальнейшего возникновения молний.
Интересно отметить, что минимально возможный размер молний в облаке связан с дисперсностью вулканического аэрозоля. Реально эта связь, конечно, носит статистический характер и использовать ее можно лишь при тщательном счете и анализе размеров всех молний, прошедших в облаке.
Каждая молния разряжает вполне определенный заряд, а это значит, что, подсчитав количество молний и их длины, нетрудно оценить величину суммарного разделенного равновесного заряда и на этом основании оценить энергию взрыва.
Для непрерывной эксплозивной струи аналогичным образом оценивается средняя мощность струи.
В заключение приведем примерный расчет энергии и мощности извержения по интенсивности электрической деятельности вулкана.
Пусть вулкан извергается в пульсирующем режиме: на фоне непрерывной сравнительно слабой гаэопепловой струи наблюдаются почти регулярные взрывы со средним интервалом D t (с), выносящие основную массу материала. Измерения кинетики роста вулканической постройки, как это сделано, например, в работах [31, 32], позволяют определить среднюю скорость выноса твердого вещества P1(кг/с). Дистанционные измерения или визуальные наблюдения цвета струи на выходе из жерла дают сведения о начальной температуре То вылетающего материала. Визуальные наблюдения (а также обработка кинограмм извержения или магнитофонной записи разрядов в радиодиапазоне) позволяют подсчитать среднюю частоту появления крупных IK (~1 — 2 км), средних Ic (0,2 — 1 км) и мелких Iм (50 — 200 м) молний (с-1) в облаке. При этом следует ввести поправку на коэффициент видимости молний h M, который имеет неодинаковую величину для молний различного размера. Положим, что молния длиной Iиз непрозрачного газопеплового облака видна только в том случае, если она состоялась со стороны, видимой наблюдателю, на глубине не более l от внешней поверхности облака; тогда коэффициент видимости h м в первом приближении пропорционален отношению длины l молнии к характерному размеру L облака:
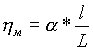 |
(3.7) |
Коэффициент пропорциональности a * зависит от формы облака. Он равен 1 для плоской ленты, 2 — для цилиндрического облака и 3 — для сферического; последние две цифры справедливы при I << L и уменьшаются по мере увеличения отношения l/L. Реальная форма газопеплового облака вначале (струя) ближе к цилиндрической, затем в зонах I и II - к сферической и, наконец, в зоне III ветрового сноса—к плоской. Однако из-за многочисленности последовательных выбросов общая форма вулканического облака все же ближе к цилиндрической (точнее, конической), и разумно для величины a* принять значение 2. Характерный размер облака (его поперечник) выберем равным 2 км (это же — и максимальный размер молнии). В результате расчетная формула принимает вид:
| (3.8) |
Теперь можно подсчитать "электрическую активность" извержения. За время Dt разрядилось ik*Dt крупных молний (средняя длина 1,5 км = 1,5.105 см), lcDt средних молний (средняя длина 6.104 см) и lMDt мелких молний (средняя длина 1,25.104 см). Воспользовавшись формулой (3.1), можно для заряда, выразившегося в молниях, записать:
| (3.9) |
В этой формуле величины lк,lс и lм соответствуют полному числу молний в облаке. Если подсчет ведется только для видимых молний, с учетом (3.8) формула несколько видоизменяется:
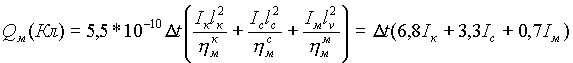 |
(3.10) |
Выше мы обсуждали вопрос о том, какая часть разделенного заряда выражается в молниях. Полагая "коэффициент использования заряда" равным 0,05, можно получить, что для каждого выброса разделенный заряд составляет:
| (3.11) |
или при подсчете видимых молний исходя из (3.10):
| (3.12) |
Пусть температура выброса Т0 такова, что ролью термоэмиссионного механизма можно пренебречь (Т < 1200 К). Тогда, воспользовавшись формулой (2.29), можно определить дисперсность аэрозоля:
| (3.13) |
и, наконец, учитывая связь Dmin с энергией взрыва Евзр [см. (1.6)], получим:
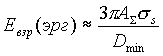 |
(3.14) |
Константу АS рассчитывали в разд. 1 для массы выброса 300 т, она составляла 8,7.103 кг. Очевидно, в нашем случае AS = - 8.7.103 [кг] (Р1 D t)/(3.105 (кг)) = 2,9.10-2 • Р1 *D t [кг]. Подставляя АS и Dmin в (3.14), получим окончательную формулу для оценки энергии взрывов:
| (3.15) |
Разделенный заряд Qp(Кл) вычисляется по (3.11) и (3.12). Поскольку средний интервал между выбросами D t в явном виде входит в окончательную формулу, формула для средней мощности извержения отличается от (3.15) только отсутствием множителя D t в числителе.
Из анализа видно, что для проведения необходимых расчетов обязательно нужен комплексный характер измерений: 1) электрической активности при извержении, 2) начальной температуры выброса, 3) кинетики выноса массы. К сожалению, известные экспериментальные работы по изучению электрической активности газопепловых туч во время извержений [15, 3] не дают достаточной информации. По-видимому, целесообразно количество и размер молний в вулканических тучах измерять несколькими синхронными приемниками радиоизлучения молний, расположенными на больших расстояниях.
В заключение авторы приносят глубокую благодарность В.М. Галицкому, Л.С. Мордовиной и А.А. Киршу за плодотворные дискуссии, а также Б.А. Трубникову, стимулировавшему проведение данной работы.
ПРИЛОЖЕНИЕ
РАСЧЕТ СКОРОСТИ ВЫСАЖИВАНИЯ ИОНОВ ИЗ ГАЗА НА АЭРОЗОЛЬНЫХ ЧАСТИЦАХ В ОБЛАКЕ
Первая стадия термозмиссионного механизма электризации вулканического аэрозоля приводит к тому, что положительный заряд сосредоточивается на конденсированных частицах, отрицательный (в виде газовых ионов) — в газовой фазе. После остывания мелких частиц они перестают эмиттировать и, наоборот, могут захватывать не только то, что они эмиттировали, но и еще один электрон или больше. Положим, что в газопепловой струе электрическое поле составляет 1,5 В/см (это обычное поле обычной спокойной атмосферы [14]). При подвижности ионов 2 см2/(В.с) скорость иона в таком поле составляет vэ = 3 см/с. Если положить, что сечение взаимодействия иона с частицей определяется размером "средней" частицы облака, то оно составит sа = p /4 D2 = 0,78. (3,2.10-4)2 = 8.10-8 см2. Для вероятности встречи иона с аэрозольной частицей, равной 0,37 = 1/е, нужно, чтобы движущийся ион "проверил" объем 1/nа, где nа — счетная концентрация аэрозоля в струе, составляющая 1,25.109 см-3. Для этого иону потребуется время, равное:
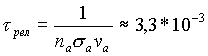 [c] [c] |
(П.1) |
В более разреженном аэрозоле время релаксации заряда в газе увеличивается обратно пропорционально счетной концентрации аэрозоля. Одновременно повышаются электрическое поле (все-таки там уже появляются молнии, т.е. среднее поле превышает 300 В/см) и скорость ионов, так что скорее всего время релаксации заряда в газе имеет величину 10-3 — 10-2 с для всех частей вулканической тучи.
Струя выброса летит до зоны I в течение 2 — 3 с. Это значит, что вторая стадия термоэмиссии начнется еще в струе [см. (2.11)]. Если задаться снижением концентрации ионов в газе на 3 порядка, это будет соответствовать времени t = З/lg еt рел. = 2,4.10-2 с, т.е. при звуковой скорости истечения — высоте ~8 м.
Равновесную концентрацию газовых ионов на второй стадии термоэмиссии (большие частицы эмиттируют, мелкие - поглощают) можно оценить из приближенного соотношения:
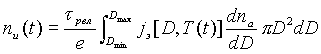 |
(П.2) |
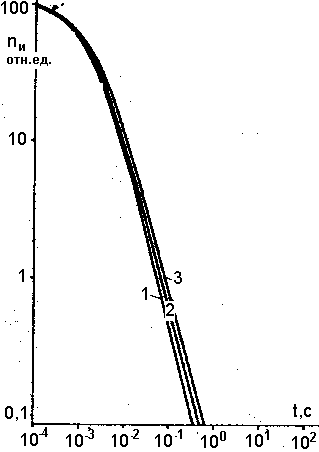 |
Рис. 19. Зависимость концентрации газовых ионов, отн. ед., от времени на второй стадии термоэмиссии, когда большие частицы эмиттируют электроны, а малые - поглощают, при разных начальных температурах выброса Т0, К; 1 - 800; 2 - 1300; 3 - 1800. |
Соотношение (П.2) справедливо только при условии, что изменение j(t) происходит медленнее, чем релаксация заряда в газе. Сопоставляя t рел со скоростью остывания частиц (см. рис. 8), можно заключить, что, уже через (5 — 10).10-2 с, т.е. на высоте ~ 30 м соотношение (П.2) выполняется с достаточной для оценок степенью точности и концентрация ионов в газе во много раз ниже, чем на первой стадии термоэмиссии. Это подтверждается рис. 19, на котором показан временной ход концентрации газовых ионов, рассчитанный для нескольких начальных температур Т0 выброса. Видно также, что начальная температура аэрозоля практически не влияет на кинетику процесса.
Список литературы
1. Шонланд Б. Полет молнии/Пер. с англ. — М.: Гидрометеоиздат, 1970.
2. Фейнман Р., Лайтон Р., Сэндс М. Фейнмановскив лекции по физике. Т. 5: Электричество и магнетизм/Пер, с англ. — М.: Мир, 1966, с. 172 - 195.
3. Руленко О.П., Токарев П.И., Фирстов П.П. Электричество вулканов. - Бюл. вулканол. станций, 1976, № 52, с. 11 — 17.
4. Земцов А.Н., Тронь А.А., Мархинин Е.К. Об электрических разрядах в пепло-газовых тучах, возникающих при вулканических извержениях. — Там же, с. 18 — 23.
б. Фукс Н.А. Механика аэрозолей. М.: Изд-во АН СССР, 1955, с. 28.
6. Уайтлоу-Грэй Р., Паттерсон X. Дым. Исследования в области аэродисперсных систем/Пер, с англ. - М. —Л.: Госхимтехиздат, 1934.
7. Трубников Б.А., Адамчук Ю.В. Сопоставление спектра масс шлако-пепловых выбросов вулканов со спектром метеоритных частиц. -Вулканология и сейсмология, 1982, № 2, с. 101 — 104; Препринт ИАЭ-2840. - М., 1977.
8. Юнге X. Химический состав и радиоактивность атмосферы/Пер. с англ. - М.: Мир, 1965, с. 140 - 141.
9. Адам Н.К. Физика и химия поверхностей/Пер, с англ, — М. — Л.: Гостехиздат, 1947.
10. Таблицы физических величин/Под ред. акад. И.К. Кикоина. — М.: Атомиэдат, 1976.
11. Мархинин Е.К. Роль вулканизма в формировании земной коры (на примере Курильской островной дуги). — М.: Наука, 1967, с. 16^.
12. Goldstein S. The Steady Flow of Viscous Fluid past a fiixed Spherical Obstacle at Small Reynolds Numbers. — Proc. Roy,: Soc., 1929, v. 123A, p. 225 - 235.
13. Штейнберг Г.С., Бабенко Ю.И. Экспериментальное определение скорости и плотности вулканических газов во время извержения. — ДАН СССР, 1976, т. 226, № 6, с. 1399 - 1402.
14. Мучник В.М. Физика грозы. — Л.: Гидрометеоиздат, 1974.
15. Руленко О.П., Токарев П.И. Атмосферные электрические эффекты Большого трещинного Толбачинского извержения в июне — октябре 1975 г. - Бюл. вулканол. станций, 1979, № 56, с. 96 - 102.
16. Левин Л.М. Исследования по физике грубодисперсных систем. — М.: Изд-во АН СССР, 1961. - 266.
17. Волощук В.М., Седунов Ю.С. Процессы коагуляции в дисперсных системах. — Л.: Гидрометеоиздат, 1975.
18. Справочник физических констант горных пород/Под ред. С. Кларка. Пер. с англ. - М.: Мир, 1969, с. 438.
19. Краткий физико-технический справочник/Под ред. К.П. Яковлева. Т. 3. - М.: Физматгиз, 1962, с. 212.
20. Будников В.А., Малеев Е.Ф., Овсянников А.А. Сравнительная характеристика пеплов Северного и Южного прорывов БТТИ 1975 — 1976 гг. - Бюл. вулканол. станций, 1979, № 56, с. 131 - 141.
21. Кэй Дж., Лэби Т. Таблицы физических и химических постоянных/Пер, с 12-го англ. изд. — М.: Изд-во физ.-мат. лит., 1962.
22. Русинов Б.Ш. Электрические и магнитные поля в атмосфере и литосфере и их использование для геологических целей: Автореферат дисс. на соиск. учен. степ. канд. геол.-минерал. наук. — Л.: Изд-во ЛГУ, 1970, с. 12.
23. Имянитов И.М. К вопросу об электризации облачных частиц после разрыва контакта между ними. — Тр. Главной геофизической обсерватории. - Л.: Гидрометеоиздат, 1969, вып. 242, с. 82 - 88.
24. Adamchuk Yu.V., Troubnikov В.A. Electrical Conductivity of Flowing Lava of the South Novo-Tolbachinsky Eruption. — Mod. Geology, 1979, v. 7, № 1, p. 37 - 41; Адамчук Ю.В., Трубников Б.А. Электропроводность текущей лавы Южного прорыва Большого трещинного Толбачинского извержения. — Вулканология и сейсмология, 1181, № 6, с. 112 - 115; Препринт ИАЭ-2841. - М., 1977.
25. Мархинин Е.К. Вулканы и жизнь (проблемы биовулканологии). — М.: Мысль, 1980, с. 118 - 119.
26. Hatakeyama H., Uchikawa К. On the disturbance of the atmospheric potential gradient caused by the eruption — smoke of the volcano Aso. - Papers in meteorology and geophysics, 1951, v. 2, № 1, p. 85 - 89.
27. Милин Б.В., Малахов С.Г. Проводимость воздуха и турбулентное перемешивание в атмосфере. — Изв. АН СССР. Сер. геофиз., 195J, № 3, с. 264 - 270.
28. Брикар Дж. Влияние радиоактивности и загрязнений на элементы атмосферного электричества. — В кн.: Проблемы атмосферного электричества (Тр. Ill Междунар. конф. по электричеству атмосферы и космического пространства. Монтре, Швейцария, 5—10 мая 1963 г)/Пер. с англ. - Л.: Гидрометеоиздат, 1969, с. 146-164.
29. Имянитов И.М., Чубарина Е.В., Шварц Я.М. Электричество облаков. — Л.: Гидрометеоиздат, 1971.
30. Казимир Г, Грозовое облако. — В кн.: Проблемы атмосферного апектричества. (Тр. III Междунар. конф. по электрич. атмосферы и космического пространства. Монтре, Швейцария, 5—10 мая 1963 г.)/Пер. с англ. - Л.: Гидрометеоиздат. 1969, с 146 - 164. I.
31. Токарев П.И. Расчет расхода магмы, роста высоты насыпного конуса и размеров подводящего канала первого кратера Большого трещинного Толбачинского извержения в июле 1975 г. — В кн.: Геологические и геофизические данные о Большом трещинном Толбачинском извержении 1975 - 1976 г. - М.: Наука, 1978, с. 23 - 27.
32. Магуськин М.А., Энман В.Б., Целищев B.C. Изменения высоты, объема и формы новых Толбачинских вулканов Северного прорыва. - там же, с. 217 - 224.
Опубликовано в виде препринта ИАЭ-4016/1, 1984